Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 4.Problemas - Ex. 71

A haste prismática mostrada é feita de aço considerado elastoplástico com E = 200   G P a e σ e = 280   M P a . Sabendo que os momentos aplicados M   e   M ’   d e   525   N m são orientados paralelamente ao eixo y , determine.

  1. A espessura do núcleo elástico
  2. O raio de curvatura da barra

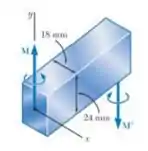
Passo 1

A espessura do nosso núcleo elástico é dada por aquele nossa terminho dado pelo símbolo y e , que podemos encontrar na seguinte equação

M = 3 2 M e 1 - 1 3 y e y 2  

Se isolarmos ele na equação, teremos que:

y e = y 3 - 2 M M e

Olhando a nossa seção, e veja que iremos colocar o nosso momento na horizontal porque vamos girar a seção, e assim poderemos fazer o cálculo do jeito que sabemos fazer, teremos que:

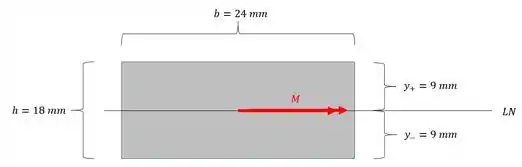
E veja que assim obtivemos o valor de y que precisávamos:

y = 9   m m

E veja o seguinte, pelo desenho do enunciado, obtemos o seguinte momento fletor atuante:

M = 525   N ∙ m

E agora só falta o nosso momento máximo elástico, assim vamos ver isso no próximo passo.

Passo 2

Sabemos que, M e é o m a x i m o   m o m e n t o   e l á s t i c o , que podemos determinar pela seguinte equação:

M e = σ e I y

Sabemos que o momento de inércia da seção é dado por:

I = b h 3 12 = 24 × 18 3 12 = 11664   m m 4

y = 9   m m

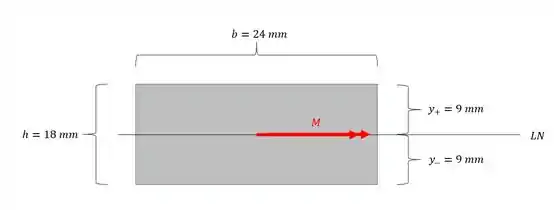
E temos no enunciado que:

σ e = 280   M P a = 280 N m m 2

M e = 280 N m m 2 11664   m m 4 9   [ m m ] = 362880   N m m = 362,88   N m

Agora temos o que é necessário para a nossa fórmula principal, assim teremos que:

y e = 9 [ m m ] 3 - 2 × 525   [ N m ] 362,88   [ N m ]

y e = 2,93   m m

E temos que lembrar que y e é a metade da espessura do núcleo elástico, assim teremos que a espessura do núcleo elástico dado por:

t = 2 y e = 2 × 2,93 = 5,86   m m

E assim resolvemos o item a).

Passo 3

E pro raio de curvatura, temos que lembrar da seguinte relação de equações, assim temos que:

ε e = y e ρ = σ e E

Assim podemos usar a seguinte relação de equações:

y e ρ = σ e E

ρ = y e E σ e

Sabemos que:

σ e = 280   M P a = 280 N m m 2

y e = 2,93   m m

E = 200   G P a = 200000   M P a = 200000 N m m 2

ρ = 2,93   m m × 200000 N m m 2 280 N m m 2

ρ = 2093   m m = 2,09   m

Resposta

  1. t = 2 y e = 5,86   m m

  2. ρ = 2093   m m = 2,09   m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A barra tem espessura de 12,5 mm e está sujeita a um momento de 90 N.m. Determine a tensão de flexão máxima na barra.
Determine o comprimento L da porção da barra de modo que as tensões de flexão máximas em A, B e C sejam as mesmas. A barra tem espessura de 10 mm.
Determine a tensão de flexão máxima desenvolvida na barra se ela for submetida aos conjugados mostrados na figura. A barra tem espessura de 6 mm.
Uma barra retangular de aço A-36 tem largura 25 mm e altura 75 mm. Determine o momento aplicado em torno do eixo horizontal que provocará o escoamento de metade da barra, considerando σe = 250 MPa.
A viga é feita de um material elástico perfeitamente plástico. Determine o momento elástico máximo e o momento plástico que podem ser aplicados à seção transversal. Considere a = 50 mm e σe = 230 MPa.