Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 18.Problemas de Revisão - Ex. 149

Uma haste uniforme de massa me comprimento 5a é dobrada na forma mostrada e é suspensa de um fio preso em B. Sabendo que a haste é atingida em C na direção z negativa e denotando o impulso correspondente por - ( F Δ t ) k , , determine imediatamente após o impacto (a) a velocidade angular da barra, (h) a velocidade de seu centro de massa G.

Passo 1

O enunciado pede que a gente imediatamente após o impacto (a) a velocidade angular do disco, (h) a velocidade de seu centro de massa G.

Vamos trazer todas as informações de inércia e momento do livro para conseguirmos calcular

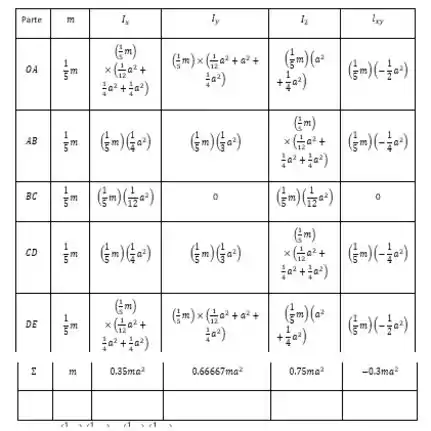
I x z = 1 5 m 1 2 x 2 + 1 5 m 1 2 a 2 = 0.2 m a 2 I y z = 1 5 m - 1 4 a 2 + 1 5 m - 1 4 a 2 = - 0.1 m a 2

Passo 2

Agora podemos determinar o momento angular sobre o centro de massa

H G x = I x ω x - I x y ω y - I x z ω z = 0.35 m a 2 ω x + 0.3 m a 2 ω y - 0.2 m a 2 ω z

H G y = - I x 1 ω x + l y ω y - I y z ω z = 0.3 m a 2 ω x + 0,66667 m a 2 ω y + 0.1 m a 2 ω z

H G z = - I x z ω x - I y z ω z + I 2 ω z = 0.1 m a 2 ω x + 0.2 m a 2 ω y + 0.75 m a 2 ω z

Restrição do cabo de suporte v - y = 0

Antes do impacto

v ¯ = 0 , H G = 0

Passo 3

(a) Momento angular, momento sobre G

r A / G × F Δ t = H G

- a 2 j × [ - ( F Δ t ) k ] = 1 2 a F Δ t i = H G x i + H G y j + H G z k

Usando expressões para H G x , H G y ' ,  e  H G z e resolvendo nos componentes

i : 1 2 a F Δ t = 0.35 m a 2 ω x + 0.3 m a 2 ω y - 0.2 m a 2 ω 2

j:  0 = 0.3 m a 2 ω x + 0.66667 m a 2 ω y + 0.1 m a 2 ω z

k:  0 = - 0.2 m a 2 ω x + 0.1 m a 2 ω y + 0.75 m a 2 ω z

resolvendo

ω x = 3.75 ( F Δ t ) m , ω y = - 1.875 ( F Δ t ) m , ω z = 1.25 ( F Δ t ) m a

ω = F Δ t m a ( 3.75 i - 1.875 j + 1.250 k )

Passo 4

(b) momento linear

F ( Δ t ) + T Δ j = m v ¯

0 = m v ¯ x , 0 + T Δ t = 0 , - F Δ t = m v ¯ z

v ¯ x = 0 , T Δ T = 0 , v ¯ z = - F Δ t m

v ¯ = - ( F Δ t / m ) k

Resposta

a ω = F Δ t m a ( 3.75 i - 1.875 j + 1.250 k )

(b) v ¯ = - ( F Δ t / m ) k

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a energia cinética do disco do Problema 18.6.
Para a placa do Problema 18.31, determine (a) a velocidade de seu centro de massa G imediatamente após o impacto, (b) o impulso exercido sobre a placa pela obstrução durante o impacto.
Uma placa retangular de massa m cai com velocidade v - 0 e sem velocidade angular quando seu canto C bate em uma obstrução. Admitindo que o impacto seja perfeitamente plástico (e = 0), determine a vel
Determine o impulso exercido sobre a placa do Problema 18.29 durante o impacto (a) pela obstrução no ponto B, (b) pelo apoio no ponto A.
O disco fino de massa m = 4 kg gira com uma velocidade angular ω 2 em relação ao braço OA, que por sua vez gira com uma velocidade angular ω 1 em torno do eixo y. Determine (a) o binário M 1j , que po