Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 18.Problemas - Ex. 31

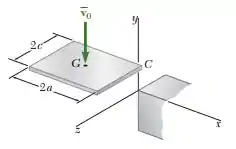
Uma placa retangular de massa m cai com velocidade v - 0 e sem velocidade angular quando seu canto C bate em uma obstrução. Admitindo que o impacto seja perfeitamente plástico (e = 0), determine a velocidade angular da placa imediatamente após o impacto.

Passo 1

Vamos lá resolver mais essa. Vamos utilizar inicialmente o princípio de impulso e quantidade de movimento linear. Para o ponto G, temos:

- m v 0 j → + F c Δ t j → = m v x i → + m v y j → + m v z k →

Para cada componente, temos:

0 = m v x → v x = 0

- m v 0 + F C Δ t = m v y → F C Δ t = m v 0 + v y

0 = m v z → v z = 0

Passo 2

Como o impacto é perfeitamente plástico, v C y = 0 . A velocidade do ponto C é dada por

v → C = v → G + ω → × r → C / G = v y j → + ω x i → + ω y j → + ω z k → × a i → - c k →

v C x i → + v C z k → =   - c ω y i → + v y + c ω x + a ω z j → - a ω y k →

Para a componente j → :

v C + c ω x + a ω z → v y = - c ω x - a ω z

Analisando os momentos em C:

c m v 0 i → + a m v 0 k → = H G x i → + H G y j → + H G z k → + - a i → + c k → × m v y j → = 2 3 m c 2 ω x i → + 2 3 m c 2 + a 2 ω y j → + 2 3 m a 2 ω z k → - m c v y i → - m a v y k →

Para cada componente:

c m v 0 = 1 3 m c 2 ω x - m c v y         ( 1 )

0 = 1 3 m c 2 + a 2 ω y → ω y = 0

a m v 0 = 1 3 m a 2 ω z - m a v y           ( 2 )

Passo 3

Como v y = - c ω x - a ω z , substituindo nas equações 1 e 2:

4 3 c ω x + a ω z = v 0

c ω x + 4 3 a ω z = v 0

Resolvendo o sistema

ω x = 3 7 c v 0

ω z = 3 7 a v 0

Logo

ω → = 3 7 v 0 1 c i → + 1 a k →

Resposta

ω → = 3 7 v 0 1 c i → + 1 a k →

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um disco homogêneo de raio de 180 mm é soldado a uma haste AG de 360 ​​mm de comprimento e de massa desprezível, que é conectada por uma manilha a uma vertical AB. A haste e o disco podem girar livrem
Resolva o problema de amostra 18.6 assumindo que o meteorito ataca p satélite em C com velocidade inicial v θ = ( 2000 m / s ) i
Uma moeda é lançada ao ar. Observa-se girar a uma taxa de 600 rpm em torno de um eixo GC perpendicular à moeda e processar em torno da direção vertical GD. Sabendo que GC forma um ângulo de 15° com GD
Um cubo sólido do lado c = 120 mm é preso como mostrado a um cabo AB de comprimento 240 mm. O cubo gira em torno de sua diagonal BC e processa em torno do eixo vertical AD. Sabendo que θ = 25 ∘ e β =
Um registro fotográfico de alta velocidade mostra que um determinado projétil foi disparado com uma velocidade horizontal V de 600 m / se com seu eixo de simetria formando um ângulo β = 3 ∘ com a hori