Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 11.Problemas de Revisão - Ex. 133

Uma haste uniforme de rigidez à flexão E I é carregada conforme mostrado. Determine ( a ) a deflexão horizontal no ponto D , ( b ) a declividade do ponto D .

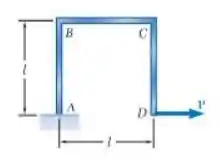
Passo 1

Fala, galerinha. Beleza? Bora pra mais um exercício.

Primeiro, vamos determinar as reações nos apoios:

∑ F y = 0 A y = 0

E também:

∑ F x = 0 A x = - P

∑ M = 0 M A = M 0

Passo 2

Em seguida, vamos determinar o momento fletor para o braço A B :

M = M A + A y = M D + P y

Logo:

∂ M P = y ∂ M ∂ M D = 1

Portanto, a energia de deformação vai ser:

U A B = ∫ 0 1   M 2 2 E I d x

Substituindo, vamos encontrar a deflexão para este braço:

∂ U A B ∂ P = 1 E I ∫ 0 1   M ∂ M P   d y = 0 ∂ U A B ∂ P = P L 3 3 E I

E para a inclinação, temos:

∂ U B C ∂ M 0 = 1 E I ∫ 0 1   M ∂ M M 0   d y = 0 ∂ U B C ∂ M 0 = P L 2 2 E I

Vamos repetir o processo para o braço B C . O momento fletor vai ser:

M = M A + A L = M D + P L

Logo:

∂ M P = L ∂ M ∂ M D = 1

Portanto, a energia de deformação vai ser:

U B C = ∫ 0 1   M 2 2 E I d x

Substituindo, vamos encontrar a deflexão para este braço:

∂ U B C ∂ P = 1 E I ∫ 0 1   M ∂ M P   d y = 0 ∂ U B C ∂ P = P L 3 3 E I

E para a inclinação, temos:

∂ U B C ∂ M 0 = 1 E I ∫ 0 1   M ∂ M M 0   d y = 0 ∂ U B C ∂ M 0 = P L 2 2 E I

E para o braço C D , o momento fletor vai ser:

M = M D + P y

Logo:

∂ M P = y ∂ M ∂ M D = 1

Portanto, a energia de deformação vai ser:

U C D = ∫ 0 1   M 2 2 E I d x

Substituindo, vamos encontrar a deflexão para este braço:

∂ U C D ∂ P = 1 E I ∫ 0 1   M ∂ M P   d y = 0 ∂ U C D ∂ P = P L 3 3 E I

E para a inclinação, temos:

∂ U C D ∂ M 0 = 1 E I ∫ 0 1   M ∂ M M 0   d y = 0 ∂ U C D ∂ M 0 = P L 2 2 E I

Passo 3

Agora, para determinarmos a deflexão no ponto D temos utilizar a seguinte relação:

δ D = ∂ U ∂ P = ∂ U A B ∂ P + ∂ U B C ∂ P + ∂ U C D ∂ P δ D = 5 P L 3 3 E I

Por fim, a inclinação no ponto D vai ser:

θ D = ∂ U ∂ M 0 = ∂ U A B ∂ M 0 + ∂ U B C ∂ M 0 + ∂ U C D ∂ M 0 θ D = 2 P L 2 E I

É isso, galera Bora pra próxima?

Resposta

δ D = 5 P L 3 3 E I

θ D = 2 P L 2 E I

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolver o Prob. 10.31, considerando que a carga 90k N é removida.
Levando em conta somente o efeito das tensões normais, determinar a energia de deformação da viga prismática A B para o carregamento mostrado.
Assumindo que a viga prismática A B tem uma seção transversal retangular, mostrar que para o carregamento dado, o máximo valor da densidade de energia de deformação específica da viga é u m = 45 8 U V
Resolver o Prob. 10.32, considerando que a carga de 30k N é removida.
Usando E = 200G P a , determinar a energia de deformação devido à flexão, para a viga com o carregamento mostrado (desprezar o efeito das tensões de cisalhamento).