Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 34
Resolver o Prob. 10.31, considerando que a carga é removida.
Passo 1
Como vocês estão, pessoal? Estão conseguindo avançar nos estudos? Então vamos fazer mais uma questão para dominar completamente o conteúdo energia de deformação.
O enunciado dessa questão pede que a gente calcule a energia de deformação combinada das duas treliças e . Essa energia de deformação combinada é a soma das energias e .
Essas duas treliças reagem a uma força que está sendo aplicada (uma força vertical de que chamaremos de ). A treliça reage com uma força e a treliça reage com uma força . É importante notar que as forças de reação das treliças e estão sempre na direção das treliças!
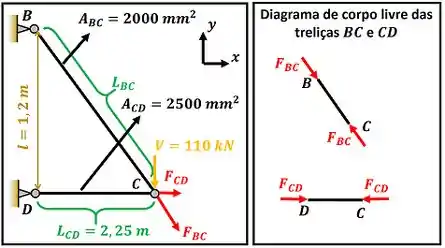
Para descobrir quanto vale e precisamos calcular quanto valem as forças e . Essas duas forças são calculadas, aplicando as equações de equilíbrio de forças nos eixos e no ponto . Tendo essas forças, calculamos e a partir das equações de energia abaixo.
é o módulo de elasticidade das treliças que vale . O módulo de elasticidade das duas treliças são iguais, porque o enunciado diz que elas são feitas do mesmo material. e são as áreas das seções transversais das treliças.
Agora que a gente sabe de tudo isso, podemos partir para o início da resolução!
Passo 2
Nesse passo, nós vamos calcular o seno e o cosseno do ângulo presente no problema.
Esses seno e cosseno de vão ser muito importantes para usar as equações de equilíbrio em e .
Veja a figura abaixo para entender que ângulo é esse.
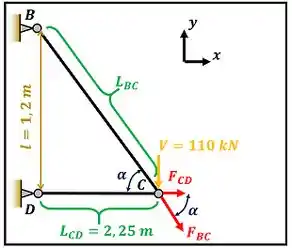
Antes de tudo, precisamos calcular o comprimento através do teorema de Pitágoras!
Para calcular o seno do ângulo , temos dividir o lado oposto ao ângulo pela hipotenusa .
Para calcular o cosseno do ângulo , temos dividir o lado adjacente ao ângulo pela hipotenusa .
Conhecendo o seno e o cosseno de podemos calcular as forças através das equações de equilíbrio em e .
Passo 3
Vamos começar o cálculo das forças fazendo o equilíbrio de forças na vertical.
são as projeções verticais (em ) das forças!
Começar pelo equilíbrio em . Tanto faz por qual equilíbrio começamos. Poderíamos começar com o equilíbrio das forças na horizontal.
Para fazer o equilíbrio vertical, vamos ver quanto vale a projeção de em .
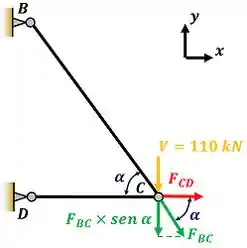
As forças que estão pra baixo na figura vão ganhar um sinal de menos e as que estão pra cima, ganham um sinal de mais na equação de equilíbrio em .
Antes de usar a equação, temos que lembrar que a força de vale .
Passo 4
Nesse passo, vamos fazer o equilíbrio de forças na horizontal (em ) através da equação abaixo.
onde são as projeções das forças na horizontal.
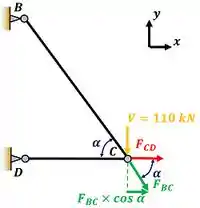
Na equação de equilíbrio em , todas as forças que estão para a esquerda ganham um sinal de menos na frente e todas as forças que estão para a direita ganham um sinal de mais na frente.
Agora temos as duas forças que precisamos para calcular , e .
No próximo passo faremos essa conta.
Passo 5
Nesse passo calcularemos , e .
Vamos começar calculando .
Antes de usar essa fórmula, temos que lembrar que a área de vale e que o módulo de elasticidade de vale .
Antes de usar a fórmula de , temos que lembrar que a área de vale .
Somando essas duas energias, somos capazes de encontrar .
Conseguiiimos! Achamos o ! Parabéns pra gente!!!