Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 11.Problemas - Ex. 69

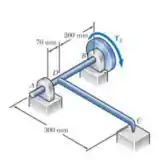
A barra de aço CD, com 20mm de diâmetro está soldada ao eixo de aço AB também com 20 mm de diâmetro conforme mostrado. A extremidade C da barra CD toca a superfície rígida mostrada quando um conjugado T B é aplicado a um disco fixado ao eixo AB. Sabendo que os mancais são auto alinhados e não exercem conjugados sobre o eixo, determine o ângulo de rotação do disco quando T B = 400   N ∙ m . Utilize E = 200 GPa e G = 77,2 GPa. (Considere a energia de deformação devido aos efeitos de flexão e torção no eixo AB e de flexão no braço CD.)

Passo 1

Galerinha, tudo bem? O enunciado pede que a gente determine o ângulo de rotação do disco quando T B = 400   N ∙ m , vamos ver os dados que temos para usarmos as fórmulas e realizar nosso cálculo, vem comigo :D

+ ↺ Σ M A B = 0 :     r C D F C = T B   F C = T B r C D

F C = 400 300 × 10 - 3 = 1333,3   N ,

F D = 1333,3   N

Passo 2

AgorA vem comigo para determinarmos o dobramento da haste CD, partiu determiner a inércia :D

I = π 4 d 2 4 = π 4 20 2 4 = 7,854 × 10 3 m m 4 = 7,854 × 10 - 9 m 4

M = F C x

A enrergia nessa seção é dada por …

U = ∫ 0 L C D F C x 2 2 E I = F C 2 L C D 3 6 E I = 1333,3 2 300 × 10 - 3 3 6 200 × 10 9 7,854 × 10 - 9 = 5,093   J

Passo 3

Agora temos que determiner a flexão do eixo ADB, começaremos determinando os momentos em A e B :D

+ ↺ Σ M B = 0 :   - F A L A B + F D b = 0     F A = F D b L A B

+ ↺ Σ M A = 0 :   + F A L A B - F D b = 0       F A = F D a L A B

Para determinarmos a energia na equação abaixo, antes temos que encontrar a inércia, vejam como fazer ;)

U = 1 2 E I ∫ 0 a F D b L A B 2 d x + ∫ 0 b F D a L A B 2 d x = F D 2 a 2 b 2 6 E I L A B

I = π 4 d 2 4 = 7.854 × 10 3 m m 4 = 7.854 × 10 - 9 m 4

L A B = 270 × 10 - 3 m

Agora sim basta substituirmos para encontrar a energia

U = ( 1333,3 ) ²   ( 70 × 10 - 3   ) ² ( 200 × 10 - 3 ) ² ( 6 ) ( 200 × 10 9   ) ( 7.854 × 10 - 9   ) ( 270 × 10 - 9   ) = 0,137 J

Passo 4

Torção: Apenas a parte DB.

J =   2 J =   15,708 × 10 - 9   m 4

U = T B 2 L D B 2 G J = 400 2 200 × 10 - 3 ( 2 ) ( 77,2   × 10 9 ) ( 15 × 708   × 10 - 9   ) = 13,194 J

Para o Total basta somarmos:

U = 5.093 +   0.137 + 13.194 =   18.424   J

1 2 T B φ B = U

Agora sim podemos determinar o ângulo, aleluiaaaa 0//

φ B = 2 U T B = 2 18,424 400 = 92,1 × 10 - 3 r a d

φ B = 5,28 °

Resposta

5,28 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Usando E = 200G P a , determinar a energia de deformação devido à flexão, para a viga com o carregamento mostrado (desprezar o efeito das tensões de cisalhamento).
Usando E = 200G P a , determinar a energia de deformação devido à flexão, para a viga com o carregamento mostrado (desprezar o efeito das tensões de cisalhamento).
Usando E = 200G P a , determinar a energia de deformação devido à flexão, para a viga com o carregamento mostrado (desprezar o efeito das tensões de cisalhamento).
Dois eixos maciços são conectados pelas duas engrenagens mostradas. Usando G = 77G P a , determinar a energia de deformação em cada um dos eixos, quando um torque T de 1130N × m é aplicado em D .
A barra de alumínio A B G = 26G P a é fortemente ligada à barra de latão B D G = 39G P a . Sabendo-se que a porção C D da barra de latão é vazada e tem um diâmetro interno de 40m m , determinar a ener