Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 172
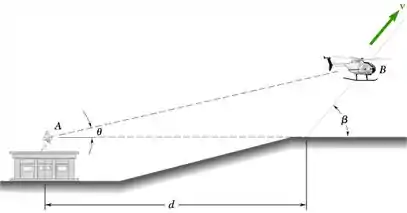
Para o helicóptero do Problema 11.169 determinou-se que, quando ele se encontrava no ponto B, a distância e o angulo de rampa desse helicóptero eram r = 900 m e = 20°, respectivamente. Quatro segundos depois, a estação de radar avistou o helicóptero na posição r = 996 m e = 23,1°. Determine a velocidade escalar media e o angulo de subida _ do helicóptero durante o intervalo de 4 s.
Passo 1
O exercício pede que a gente determine a velocidade escalar media e o angulo de subida _ do helicóptero durante o intervalo de 4 s.
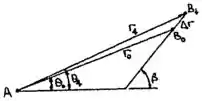
Nós temos
Passo 2
Do diagrama
Agora
Além disso,
Resposta
Exercícios de Livros Relacionados
O caminhão de 10t puxa o reboque de 20t . Se o conjunto parte do repouso em uma estrada horizontal com uma força de tração de 20k N entre as rodas do caminhão e a estrada, calcule a tração T na barra
Em um determinado instante, o caixote de 40k g tem uma velocidade de 10m / s subindo o plano inclinado a 20 ° . Calcule o tempo t necessário para o caixote atingir o repouso e a correspondente distânc
Calcule a aceleração vertical a do cilindro de 150k g para cada um dos dois casos ilustrados. Despreze o atrito e a massa de polias.
Um carro A viaja a uma velocidade constante de 100k m / h . Quando na posição mostrada no instante de tempo t = 0 , o carro B tem uma velocidade de 40k m / h e acelera a uma taxa constante de 0,1 g ao
Repita o Prob. 2/59, salvo que o carro B , em vez de possuir uma aceleração constante, agora acelera conforme mostrado no gráfico a seguir. O instante de tempo t 2 é o momento em que a velocidade perm