Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.4 - Ex. 3
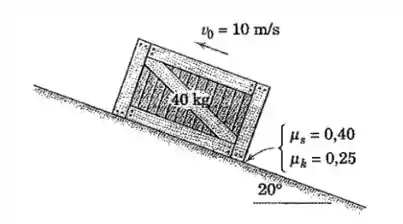
Em um determinado instante, o caixote de tem uma velocidade de subindo o plano inclinado a . Calcule o tempo necessário para o caixote atingir o repouso e a correspondente distância percorrida. Também, determine a distância percorrida quando a velocidade do caixote for reduzida para .
Passo 1
Conforme o bloco sobe o plano inclinado, sem nenhuma força para manter o movimento, ele vai ser freado tanto pelo atrito quanto pela força da gravidade.
Vamos calcular essas duas forças. Para o atrito vamos usar o coeficiente cinético, já que o bloco está em movimento:
E para a força da gravidade temos que considerar o componente paralelo ao plano:
De forma que a força resultante sobre o bloco é:
Onde consideramos o sentido negativo como sendo plano abaixo.
Passo 2
Agora vamos ver qual é a aceleração produzida por essa força sobre o bloco:
E agora é só usar a equação de Torricelli para calcular a distância percorrida pelo bloco até parar:
E quando consideramos a distância ercorrida só até a velocidade cair para :
Passo 3
E agora para calcular o tempo até a parada é só fazer o seguinte:
Pronto!
Resposta
O tempo até a parada é e as distâncias percorridas são e .