Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 168

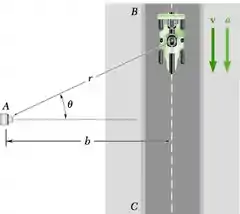
Determine a intensidade da aceleração do carro de corrida do Problema 11.167 em termos de θ , θ ˙ e θ ¨ .

Passo 1

E ai gurizada tudo bem? O enunciado pede que a gente determine a intensidade da aceleração do carro

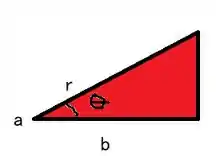
Nós temos

r = b cos ⁡ θ

Então

r ˙ = b θ ˙ sin ⁡ θ cos 2   θ

Passo 2

Para o movimento retilíneo da solução

a = d v d t

Da solução para o Problema 11.167

v = - b θ ˙ cos 2   θ

Então

a = d d t - b θ ˙ cos 2   θ = - b θ ¨ cos 2 θ - θ ˙ - 2 θ ˙ cos ⁡ θ sin ⁡ θ cos 4   θ

Passo 3

Solução alternativa.

De cima

r = b cos ⁡ θ             r ˙ = b θ ˙ sin ⁡ θ cos 2   θ

Então

r ¨ = b θ ¨ sin ⁡ θ + θ ˙ 2 cos ⁡ θ cos 2   θ - θ ˙ sin ⁡ θ - 2 θ ˙ cos ⁡ θ sin ⁡ θ cos 4   θ

= b θ ¨ sin ⁡ θ cos 2   θ + θ ˙ 2 1 + sin 2   θ cos 3   θ

Agora

a 2 = a r 2 + a θ 2

onde

a r = r ¨ - r θ ˙ 2 = b θ ¨ sin ⁡ θ cos 2   θ + θ ˙ 2 1 + sin 2   θ cos 2   θ - b θ ˙ 2 cos ⁡ θ = b cos 2   θ θ ¨ sin ⁡ θ + 2 θ ˙   sin 2   θ cos ⁡ θ

a r = b sin ⁡ θ cos 2   θ θ ¨ + 2 θ ˙ 2 tan ⁡ θ

e

a θ = r θ ¨ + 2 r ˙ θ ˙ = b θ ¨ cos ⁡ θ + 2 b θ ˙ sin ⁡ θ cos 2   θ

= b cos ⁡ θ cos 2   θ θ ¨ + 2 θ ˙ tan ⁡ θ

Passo 4

Então

a = ± b cos 2   θ θ ¨ + 2 θ ˙ 2 tan ⁡ θ [ ( sin ⁡ θ ) 2 + ( cos ⁡ θ ) 2 ] 1 / 2

Para a posição do carro mostrado, θ ¨ é negativo; para a ser positivo, a raiz negativa é escolhida.

Resposta

a = - c cos 2   θ θ ¨ + 2 θ ˙ 2 tan ⁡ θ

a = - b cos 2   θ θ ¨ + 2 θ ˙ 2 tan ⁡ θ

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O caixote de 50k g está parado quando a força P é aplicada. Determine a aceleração resultante do caixote se (a) P = 0 , (b) P = 150N e (c) P = 300N .
O avião a jato de 300t possui três motores, cada um deles produz um empuxo quase constante de 240k N durante a decolagem. Determine o comprimento s necessário da pista se a velocidade de decolagem é d
O homem de 80k g em uma cadeira para trabalhos em altura exerce uma força de tração de 270N sobre a corda por um curto intervalo de tempo. Encontre a sua aceleração. Despreze a massa da cadeira, da co
Um homem puxa a si mesmo para cima no plano inclinado com 15 ° pelo método mostrado. Se a massa combinada do homem e do carrinho é de 100k g , determine a aceleração do carrinho quando o homem exerce
Um esquiador parte do repouso sobre uma encosta com 40 ° no instante de tempo t = 0 e registra o tempo t = 2,58s quando passa um ponto de controle da velocidade 20 metros abaixo na encosta. Determine