Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.4 - Ex. 7
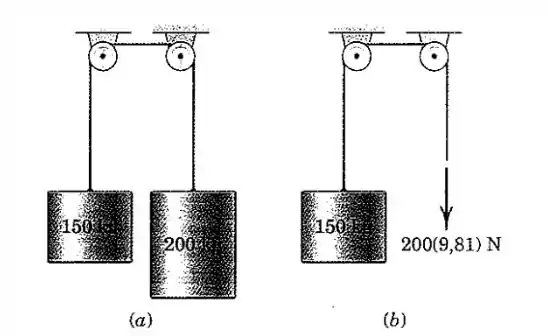
Calcule a aceleração vertical do cilindro de para cada um dos dois casos ilustrados. Despreze o atrito e a massa de polias.
Passo 1
Vamoas analisar o caso (a). A situação é a seguinte:
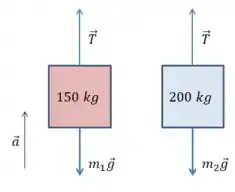
Como os dois blocos estão ligados pelo mesmo cabo, a tensão nos dois lados é a mesma. E estamos considerando que o sentido positivo da aceleração acompanha a subida do bloco de .
Aplicando a segunda lei de Newton nos dois blocos, achamos o seguinte:
E agora projetamos as duas equações no eixo vertical. Isso é o mesmo que fazer o produto escalar da equação inteira pelo vetor .
O resultado é esse sistema aqui:
Passo 2
Vamos resolver esse sistema para encontrar . Subtraindo a segunda equação da primeira ficamos com o seguinte:
E essa é a aceleração do sistema, inclusive do cilindro .
Passo 3
O que muda quando, ao invés do cilindro , colocamos uma força de módulo igual ao peso do cilindro?
Bom, agora aquele cabo está simplesmente transmitindo a força, e a situação é a seguinte:
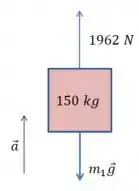
E então a segunda lei de Newton vai dar a seguinte expressão:
Resolvido!
Resposta
(a)
(b)