Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.2 - Ex. 59
Um carro viaja a uma velocidade constante de . Quando na posição mostrada no instante de tempo , o carro tem uma velocidade de e acelera a uma taxa constante de ao longo de sua trajetória até que atinja uma velocidade de , depois do que viaja em uma velocidade constante. Qual é a posição em regime permanente do carro com relação ao carro ?
Passo 1
Para determinar a posição relativa, precisamos primeiro determinar a posição de cada carro em função do tempo, beleza?
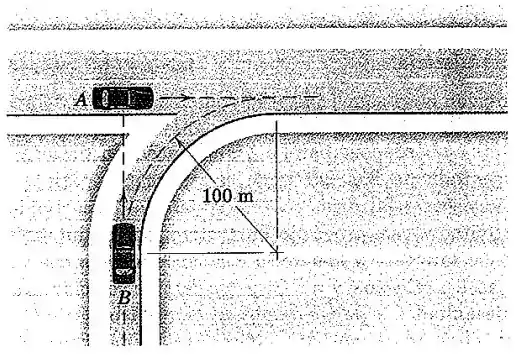
Observe que o carro faz um trajeto de um quarto de círculo de raio até chegar na horizontal, ou seja, até chegar no vértice superior direito do quadrado desenhado. Perceba que o carro chega até esse mesmo ponto por meio de um lado desse quadrado, cuja medida é também igual ao raio .
Isso significa que, se considerarmos esse vértice como a origem do nosso sistema de coordenadas, a posição inicial do carro será:
Como o carro tem uma velocidade constante , temos:
Passo 2
Para o carro , teremos dois momentos. Até o instante , que iremos calcular, o carro desenvolve uma aceleração constante , partindo de até alcançar :
Agora vamos calcular qual a posição do carro depois de :
Passo 3
Para o carro , lembre-se que antes de ele chegar à origem do sistema, ele passa por um trajeto em forma de um quarto de círculo de raio , e portanto, sua posição inicial será:
Então, vamos calcular a posição de quando :
Passo 4
Finalmente, como os carros passam a viajar com a mesma velocidade depois do instante , eles permanecem indefinidamente com a mesma distância relativa do instante . Ou seja, para o nosso objetivo, basta calcular a distância relativa entre os carros no instante :
Ou seja, em regime permanente, o carro fica sempre à frente do carro .
Resposta
à frente de por