A espessura da placa triangular varia linearmente em y, dede o valor ao longo da sua base em y = 0 até em y = h. Determine a coordenada y do centro de massa da placa.
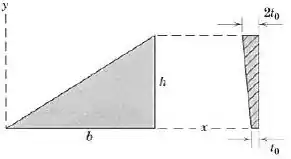
Passo 1
Sabendo que a equação para encontrar o centro de massa é dado por:
Dessa maneira, vamos primeiro encontrar a massa do problema.
Passo 2
Mas antes vamos escolher um elemento de massa, para assim podermos integrar, com isso:
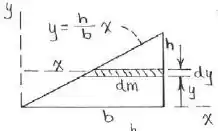
Pronto! Escolhido o elemento de massa vamos integrar ele em relação a y e temos a nossa massa. Lembre-se que:
Logo,
Como o volume varia em relação a t, temos:
Note que o nosso se o elemento de área for o mesmo que o elemento de massa, então:
Sendo assim,
Agora vamos tentar representar a variação em t com alguma relação. Observe que ele varia em y, ou seja, se teremos , mas se y=h temos . Assim,
Observe também, que a equação linear que representa a reta é dada por:
Dessa maneira, substituindo essas informações,
Simplificando:
Passo 3
Tendo a função que descreve o nosso problema fica mais fácil de integrar, dessa maneira a massa é dada por:
Agora basta resolvermos essa integral que teremos nossa massa, sendo que:
Passo 4
Ante de aplicar a equação para achar o centro de massa na coordenada y, vamos resolver a integral:
Depois é só dividir pela massa que teremos o ponto. Como já conhecemos dm é só manipulação:
Assim,
Passo 5
Agora substituindo na equação do centro de massa, temos: