Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 3.Problemas - Ex. 6
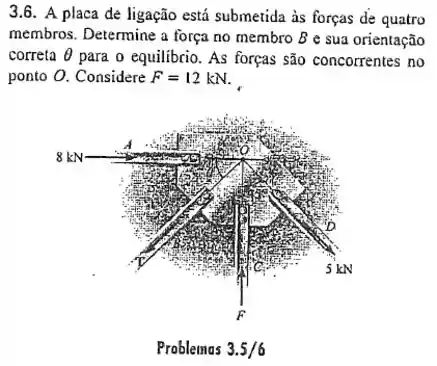
Passo 1
Como as forças são concorrentes no ponto podemos dizer que elas estão atuando sobre esse ponto, então vamos fazer o diagrama de corpo livre dele para calcularmos as intensidades das forças:
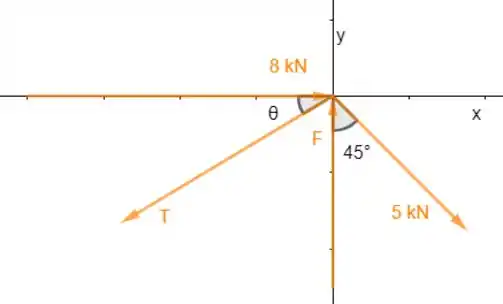
Passo 2
A soma de forças em e em deve ser zero.
Vamos decompor primeiro as forças em :
Passo 3
Agora vamos decompor as forças em para achar a força :
Sabemos o valor de e no ultimo passo descobrimos o valor de , substituindo:
Seno sobre cosseno é igual a tangente então podemos escrever:
Passo 4
Agora que temos o ângulo podemos usar a equação encontrada no Passo 2 para descobrirmos a força :
Resposta
Exercícios de Livros Relacionados
O braço regulável A B C pode ser abaixado até que a extremidade C esteja perto do chão, de modo que os operários possam embarcar facilmente na plataforma.Para a posição, quando θ = - 20 ° , determine
A posição do elemento A B C é controlada pelo cilindro hidráulico C D . Sabendo que θ = 30 ° , determine para o carregamento mostrado a a força exercida pelo cilindro hidráulico no pino, b a reação em
O braço regulável A B C é usado para movimentar uma plataforma de elevação para operários de construção. Juntos, os operários e a plataforma tem uma massa de 200 k g e um centro de gravidade combinado
A grande tenaz mecânica mostrada na figura é usada para agarrar e erguer uma placa grossa de aço H J de 7500 k g . Sabendo que não ocorre escorregamento entre as garras da tenaz e a placa em H e J , d
Resolva o problema 6.157 considerando que a força P de 9 k N atua horizontalmente para a direita θ = 0 ° .