Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 3.Problemas - Ex. 12
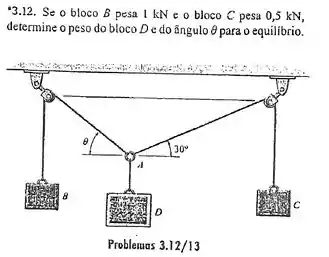
Passo 1
Vamos fazer o diagrama de corpo livre no ponto O:
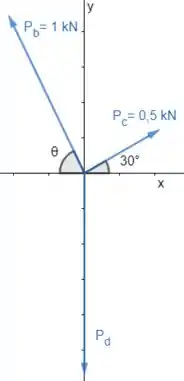
Passo 2
A soma de forças em e em deve ser zero.
Vamos decompor primeiro as forças em :
O enunciado nos fala qual é os pesos das caixas e :
Passo 3
Agora vamos decompor as forças em :
Como já temos os valores dos pesos das caixas C e D, e descobrimos no Passo anterior o valor do ângulo, podemos substituir os valores na equação e vamos chegar a respota:
Resposta
Exercícios de Livros Relacionados
Sabendo que θ = 60 , determine as reações em (a) B e (b) em C.
Para a figura a seguir, (a) determine a equação em termo dos dados fornecidos para que o sistema esteja em equilíbrio e (b) determine o valor do ângulo para equilíbrio quando M = 150 N m ,P = 200 Nel
Sabendo que θ = 30 , determine as reações em (a) B e (b) em C.
Para a figura abaixo (a) esboçe a tração no cabo em termo de θ e W e (b) determine o valor de θ tal que a tração vale 3W.
Desprezando o peso da barra AB, determine (a) a equação que deve ser satisfeita quando a haste está em equilíbrio e (b) determine o ângulo para equilíbrio quando P = 64 N ,Q = 48 N ,l = 500 m m e a =