Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 3.Problemas - Ex. 3
Passo 1
Falaaaaa galerinha do RespondeAí, tudo belezoca?
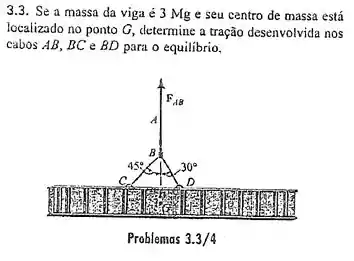
Saca só, nesse exercício aqui o enunciado nos diz que a viga de massa está em equilíbrio sobre a ação de forças que atuam através dos cabos mostrados no diagrama a seguir:
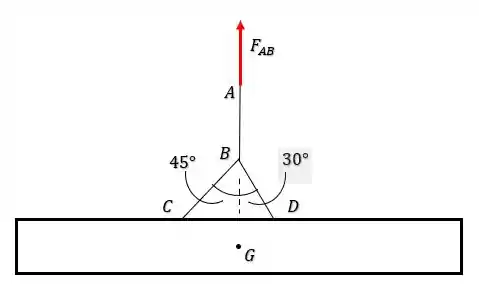
Isso quer dizer que a força está suportanto a viga inteira, então:
onde é o peso da viga.
O enunciado diz que a massa é igual a (podemos ler a unidade como “Mega-gramas”, quase nada usual) isso é igual:
Ou então em :
(Esse g da massa é de gramas, não confunda com o g da gravidade que aparece na fórmula), a equação vai ficar:
Passo 2
Iradoso, agora vamos fazer o diagrama de corpo livre para o nó em B, vai ficar mais ou menos assim:
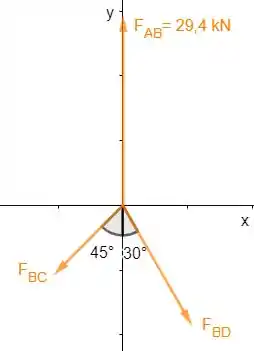
Como tudo isso ai tem que estar em equilíbrio, quer dizer que a soma de forças em e em deve ser igual a zero.
Então primeiro decompondo as forças em , vamos obter que:
Subsituindo os valores que conhecemos:
Logo:
Passo 3
Belezoca, agora vamos decompor as forças em , tal que:
Logo:
Passo 4
Maravilha, agora que já temos uma relação entre as forças, podemos substituir a equação que achamos no Passo 3 na do Passo 2, de maneira que:
Isolando :
Portanto, tem módulo dado como:
Substituindo esse valor na equação do Passo 3 vamos descobrir que:
