Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.5 - Ex. 20
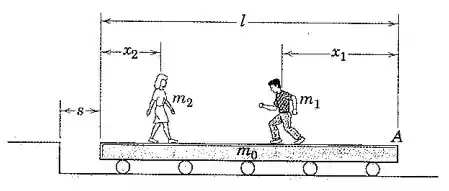
O homem de massa e a mulher de massa estão em pé sobre extremos opostos da plataforma de massa que se desloca com atrito desprezível e está inicialmente em repouso com . O homem e a mulher começam a se aproximar um do outro. Desenvolva uma expressão para o deslocamento da plataforma quando os dois se encontram em termos do deslocamento do homem em relação à plataforma.
Passo 1
Repare que as únicas forças agindo nesse caso são forças internas ao sistema. Por exemplo, o homem empurra o chão da plataforma para trás, e a plataforma reage empurrando-o para a frente, em direção à mulher.
Então, como não há forças externas, o centro de massa do sistema “plataforma-homem-mulher” relativo a um ponto fixo permanece constante. Sendo esse ponto fixo, precisamos calcular a posição do centro de massa em relação a esse ponto quando o homem e a mulher estavam em extremos opostos da plataforma.
Para isso, perceba que a plataforma tem centro de massa em , o homem se encontra em , e a mulher, em :
Passo 2
Porém, quando o homem encontra a mulher, a nova posição do centro de massa da plataforma terá deslocado para a direita:
O homem terá deslocado sua posição de para a esquerda, e também para a direita por causa do movimento da plataforma:
Além disso, a mulher se desloca para a direita e também para a direita:
Porém, como o homem e a mulher estão no mesmo ponto da plataforma, temos:
E portanto:
Passo 3
Sabendo das novas localizações dos centros de massa de cada membro do sistema, podemos calcular o centro de massa do sistema e igualar ao que obtivemos inicialmente: