Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 56

Um homem tendo massa de 75 kg senta na cadeira que está presa por um pino à estrutura BC. Se o homem está sempre sentando em uma posição vertical, determine as reações horizontal e vertical da cadeira sobre o homem no instante θ = 45 ° . Neste instante ele tem uma velocidade de 6 m/s que está acelerando a 0,5   m / s 2 .

Passo 1

A chave de problemas de cinética está no diagrama de corpo livre. Ao identificarmos todas as forças que o nosso problema está sujeito, conseguiremos visualizar o que há de ser feito mais facilmente.

Relembrando do capítulo de cinemática, vimos que a aceleração centrípeta de um corpo é dada por:

a n = v 2 ρ

Passo 2

Vamos começar por esboçar o diagrama de corpo livre. Considerando a pessoa como uma partícula o seguinte diagrama:

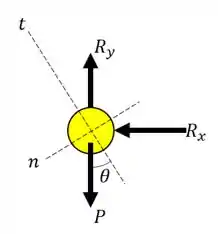
A pessoa está sujeita a duas reações da cadeira, uma vertical, devido ao assento, e uma horizontal, devido ao apoio das costas. Além disto, ele está sujeito a força peso.

Passo 3

Para podermos resolver a questão, precisamos trabalhar com as equações da cinética tanto no eixo normal, em que a pessoa está sujeita a uma aceleração normal, quanto no eixo tangencial, no qual a pessoa está sujeita a uma aceleração de 0,5   m / s 2 .

Fazendo o somatório das forças na componente normal, obtemos:

∑ F n = m ⋅ a n = m v 2 ρ

R x sen ⁡ 45 ° - R y sen ⁡ 45 ° + P sen ⁡ 45 ° = 75 ⋅ 6 2 10

R x sen ⁡ 45 ° - R y sen ⁡ 45 ° = - 250,25

Já para o eixo tangencial, temos:

∑ F t = m ⋅ a t = m v 2 ρ

R x cos ⁡ 45 ° + R y cos ⁡ 45 ° - P cos ⁡ 45 ° = 75 ⋅ 0,5

R x cos ⁡ 45 ° + R y cos ⁡ 45 ° = 557,75

Resolvendo o sistema com ambas as equações, conseguimos determinar as reações da cadeira, as quais são:

R x = 217,4   N

R y = 571,3   N

Resposta

R x = 217,4   N

R y = 571,3   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a velocidade angular constante θ ˙ do eixo vertical do brinquedo do parque de diversões se ϕ = 45 ° . Despreze a massa dos cabos e a dimensão dos passageiros.
O pino P de 0,2 kg está restrito a se mover na fenda curva lisa que é definida pela lemniscata r = ( 0,6 cos ⁡ 2 θ ) m. O seu movimento é controlado pela rotação do braço bifurcado O A , o qual tem ve
Uma bola de 0,2 kg é soprada em um tubo circular vertical liso cuja forma é definida por r = ( 0,6 sen ⁡ θ ) m, onde θ é dado em radianos. Se θ = ( π t 2 ) rad, onde t é dado em segundos, determine a
A barra A B de 2 kg desloca-se para cima e para baixo à medida que sua extremidade desliza sobre a superfície lisa do came, onde r = 0,1 m e z = ( 0,02 sen ⁡ θ ) m . Se o came está girando com velocid
Se o coeficiente de atrito estático entre a superfície cônica e o bloco de massa m é μ s = 0,2 , determine a velocidade angular constante mínima θ ˙ de maneira que o bloco não escorregue para baixo.