Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas fundamentais - Ex. 14

Uma bola de 0,2 kg é soprada em um tubo circular vertical liso cuja forma é definida por r = ( 0,6 sen ⁡ θ ) m, onde θ é dado em radianos. Se θ = ( π t 2 ) rad, onde t é dado em segundos, determine a intensidade de força F exercida pelo soprador sobre a bola quando t = 0,5 s.

Passo 1

O enunciado nos dá as seguintes informações:

Massa da bola: m = 0,2   k g

r = ( 0,6 sen ⁡ θ )   m

θ = ( π t 2 ) rad

Nosso objetivo é calcular a intensidade da força F exercida pelo soprador sobre a bola para o instante t = 0,5 s.

Vamos iniciar desenhando o diagrama de corpo livre da bola.

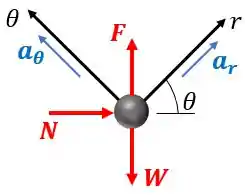
Onde W = m g é a força peso, g = 9,81   m / s 2 e N é a força normal da parede que atua perpendicularmente à trajetória da bola no instante t .

Passo 2

Primeiramente, vamos encontrar as derivadas temporais da blola em r ( r ˙ e r ¨ ):

r = ( 0,6 sen ⁡ θ ) = 0,6 sen ⁡ ( π t 2 ) m

r ˙ = d r d t = 0,6 cos ⁡ ( π t 2 ) 2 π t = 1,2 π t cos ⁡ ( π t 2 )   m / s

r ¨ = d 2 r d t 2 = [ 1,2 π cos ⁡ π t 2 - 2,4 π t 2 sen ⁡ π t 2 ]   m / s 2

Agora as derivadas temporais em θ ( θ ˙ e θ ¨ ):

θ = π t 2   r a d

θ ˙ = d θ d t = 2 π t   r a d / s

θ ¨ = d θ ˙ d t = 2 π   r a d / s 2

Para t = 0,5   s , teremos

r = 0,6 sen ⁡ ( π t 2 ) = 0,42   m

r ˙ = 1,2 π t cos ⁡ ( π t 2 ) = 1,33   m / s

r ¨ = 1,2 π cos ⁡ π t 2 - 2,4 π t 2 sen ⁡ π t 2 = - 1,53   m / s 2

θ = π t 2 = π 4   r a d

θ ˙ = 2 π t = π   r a d / s

θ ¨ = 2 π   r a d / s 2

Passo 3

Sabemos que as componentes da aceleração do bloco nas coordenadas r e θ são dadas por

a r = r ¨ - r θ ˙ 2

a θ = r θ ¨ + 2 r ˙ θ ˙

Logo,

a r = r ¨ - r θ ˙ 2 = - 1,53 - 0,42 π 2 = - 5,67   m / s 2

a θ = r θ ¨ + 2 r ˙ θ ˙ = 0,42 2 π + 2 1,33 π = 11   m / s 2

Passo 4

Agora aplicaremos as Equações do Movimento.

Nesta etapa devemos tomar cuidado pois o θ deve estar em graus, não em radianos.

θ = π 4   r a d = 45 °

Analisando primeiramente no eixo r , temos que

∑ F r = m a r

F sen ⁡ 45 ° + N cos ⁡ 45 ° - W sen ⁡ 45 ° = m a r

F sen ⁡ 45 ° + N cos ⁡ 45 ° - 0,2 9,81 sen ⁡ 45 ° = 0,2 ( - 5,67 )

F sen ⁡ 45 ° + N cos ⁡ 45 ° = 0,253

Analisando no eixo θ , temos

∑ F θ = m a θ

F cos ⁡ 45 ° - N s en ⁡ 45 ° - W cos ⁡ 45 ° = m a θ

F cos ⁡ 45 ° - N cos ⁡ 45 ° - 0,2 9,81 cos ⁡ 45 ° = 0,2 ( 11 )

F cos ⁡ 45 ° - N cos ⁡ 45 ° = 3,587

Chegamos ao sistema

F sen ⁡ 45 ° + N cos ⁡ 45 ° = 0,253 F cos ⁡ 45 ° - N cos ⁡ 45 ° = 3,587

Somando a primeira equação com a segunda, chegamos à

F ( sen ⁡ 45 ° + cos ⁡ 45 ° ) = 0 , 247 + 3,587 = 3,84

F = 2,7 2   N

Substituindo o valor de F em uma das equações, podemos encontrar o valor para N . Logo,

N cos ⁡ 45 ° = 0,253 - F sen ⁡ 45 °

N = - 2,36   N

Com o sinal de N deu negativo, seu sentido é oposto ao desenhado no diagrama de corpo livre.

Resposta

F = 2,72   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para as condições indicadas no Prob. 3 / 89 , determine as componentes inerciais x e y da força horizontal P → exercida sobre o cursor pelo tubo imediatamente antes do cursor sair do tubo. Imgem do Pr
O carro de 1500k g está viajando a 100k m / h sobre a porção reta da estrada, e então sua velocidade é reduzida uniformemente de A para C , posição em que este atinge o repouso. Calcule o módulo F da
A atração de parque de diversões consiste em um suporte fixo junto a O , do braço 6mO A , que gira em torno do eixo em O , e do compartimento, que permanece horizontal por meio de um mecanismo em A (n
Quando uma correia em V aciona uma polia em alta velocidade, a ação centrífuga tende a diminuir o seu contato com a polia e consequentemente reduzir a capacidade de transmitir torque. Um dispositivo p
Um pequeno veículo entra no topo A da trajetória circular com uma velocidade horizontal v 0 e ganha velocidade conforme se desloca pra baixo na trajetória. Determine uma expressão para o ângulo β que