Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas fundamentais - Ex. 13

Determine a velocidade angular constante θ ˙ do eixo vertical do brinquedo do parque de diversões se ϕ = 45 ° . Despreze a massa dos cabos e a dimensão dos passageiros.

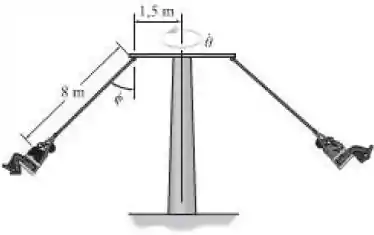
Passo 1

O enunciado nos dá o valor ϕ = 45 ° e pede para que a velocidade angular constante θ ˙ do eixo vertical seja definida.

Como θ ˙ é constante, sabemos que sua derivada no tempo será igual a zero e, através da geometria e dos comprimentos fornecidos pela imagem da questão, podemos encontrar o valor de r .

r = 1,5 + 8 sen ⁡ ϕ

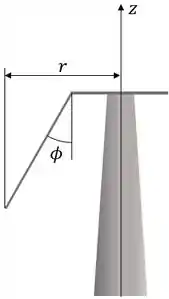
Como ϕ é definido, temos que r = 7,157   m .

Em seguida, foi desenhado o diagrama de corpo livre centralizado no passageiro.

Onde W = m g é a força peso, g = 9,81   m / s 2 é a aceleração gravitacional e T é a força exercida pelo cabo.

Passo 2

Primeiramente, vamos encontrar as derivadas temporais em r .

Para ϕ = 45 ° ,

r = 7,157   m

r ˙ = d r d t = 0   m / s

r ¨ = d 2 r d t 2 = 0   m / s 2

Agora analisaremos as derivadas temporais em θ ( θ ˙ e θ ¨ ). O valor de θ ˙ é o que queremos descobrir, porém sabemos que seu valor é constante. Logo,

θ ¨ = d θ ˙ d t = 0   r a d / s 2

Como não há variações em relação ao eixo z durante o movimento, z ˙ = z ¨ = 0 .

Passo 3

Sabemos que as componentes da aceleração do bloco nas coordenadas r , θ e z são dadas por

a r = r ¨ - r θ ˙ 2

a θ = r θ ¨ + 2 r ˙ θ ˙

a z = z ¨

Logo,

a r = r ¨ - r θ ˙ 2 = 0 - ( 7,157 ) θ ˙ 2 = - 7,157 θ ˙ 2   m / s 2

a θ = r θ ¨ + 2 r ˙ θ ˙ = 7,157 0 + 2 0 θ ˙ = 0   m / s 2

a z = z ¨ = 0   m / s 2

Passo 4

Agora aplicaremos as Equações do Movimento.

Analisando primeiramente no eixo z , temos que

∑ F z = m a z

T cos ⁡ 45 ° - W = m ( 0 )

T cos ⁡ 45 ° = W = m g

T = m g cos ⁡ 45 ° = 13,87 m

Analisando no eixo r , temos

∑ F r = m a r

- T sen ⁡ 45 ° = m - 7,157 θ ˙ 2  

θ ˙ 2 = T sen ⁡ 45 ° 7,157 m = ( 13,87 ) sen ⁡ 45 ° 7,157 m = 1,37

θ ˙ = 1,17   r a d / s

Resposta

θ ˙ = 1,17   r a d / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a velocidade v na qual o carro de corrida não terá tendência a deslizar lateralmente sobre a pista inclinada, isto é, a velocidade em que não existe dependência do atrito. Além disso, determ
O disco com a caneleta circular gira em torno do eixo vertical com uma rotação constante de 30r p m e suporta duas esferas de 4k g . Calcule a maior das duas forças de contato entre o disco e cada esf
A partir do repouso em que θ = 20 ° , uma criança de 35k g desliza com atrito desprezível para baixo no escorrega que tem a forma de um arco circular com raio de 2,5m . Determine a aceleração tangenci
A pequena esfera de massa m está presa a um fio leve de comprimento L e se desloca como um pêndulo cônico em um círculo horizontal com uma velocidade tangencial v . Localize o plano de movimento pela
Repita o Problema 3/83, exceto pelo carro estar no topo de uma elevação como mostrado na figura.