Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 7.Problemas - Ex. 113
Se a inclinação do cabo no apoio é zero, determine a curva de deflexão do cabo e a tração máxima desenvolvida nele.
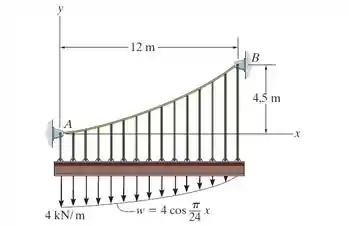
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Queremos determinar a curva de deflexão e a máxima tração desenvolvida no cabo.
A vantagem é que, para podermos determinar a máxima tração, é extremamente necessário que determinemos a curva ! Então, estamos no lucro!
Então, vamos lá! Para determinarmos a curva de deflexão, temos que resolver a seguinte integral:
Sendo o carregamento aplicado na corda. Como , então a nossa equação será:
Passo 2
Agora que obtivemos a equação da curvatura da corda, devemos aplicar as condições de contorno para descobrir as incógnitas , e .
Para a geometria da questão, temos as seguintes condições de contorno: , e .
Agora só nos resta aplicarmos as condições de contorno. Começando pela primeira, temos:
Já aplicando a segunda, obtemos:
Por fim, aplicando a terceira condição, temos:
Portanto, a equação da corda é:
E assim resolvemos a primeira parte da questão!
Passo 3
Para finalizarmos a questão, basta descobrirmos a tração máxima na corda. Esta tração ocorrerá no ponto de maior inclinação. Isto é, o ponto em que for máximo.
Para esta questão, como , então, a inclinação será máxima na extremidade em . Calculando o ângulo de inclinação, teremos:
Por fim, a tração máxima será:
E assim finalizamos a questão!