Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 7.Problemas - Ex. 115
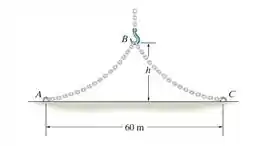
A corrente de 80 m de extensão é fixada em suas extremidades e içada em seu ponto intermediário por um guindaste. Se a corrente tem peso de , determine a altura mínima do gancho a fim de levantar a corrente completamente para fora do solo. Qual é a força horizontal no pino ou quando a corrente está nessa posição? Dica: quando é mínimo, a inclinação em e é zero.
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Queremos determinar a altura mínima do gancho a fim de levantar uma corrente de peso igual a . Sabemos que a flecha mínima ocorrerá quando a tração no cabo for a máxima.
Depois disto, vamos ter que determinar a força horizontal no pino ou , que é exatamente o valor que calcularemos ao decorrer da questão!
Bom, para que a gente possa determinar ambas as incógnitas, precisamos determinar a equação da curva que define o cabo. E para isto, como o cabo está sujeito ao próprio peso, temos que começar resolvendo a seguinte integral:
Sendo o carregamento aplicado na corrente. Para nossa alegria, já sabemos que o resultado da integração acima é:
Passo 2
Agora temos que descobrir quem as constantes da nossa equação. Para isto, teremos que aplicar as condições de contorno do problema.
Fixando o sistema de coordenadas no ponto , teremos as seguintes condições: em e . Só que possamos aplicar estas condições, temos que manipular as nossas relações
Vamos começar aplicando . Para isto, precisamos lembrar que:
Sendo esse o mesmo da equação que obtivemos no Passo 1. Então, aplicando a condição, temos:
Aplicando a condição que quando , temos:
E assim chegamos à relação:
Passo 3
Após obtermos a equação que relaciona com , já temos informação suficiente para que calculemos a força horizontal nos pontos e , que é a força .
Para que assim o façamos, basta analisarmos a geometria da questão para obter a condição que devemos utilizar.
Como a corrente possui 80 m. Pela sua simetria, temos 40 m para um lado, e 40 m para o outro. Portanto, quando , temos . Aplicando esta condição na equação obtida no Passo 2, teremos:
Resolvendo iterativamente nós obtemos que . E assim descobrimos a primeira resposta da questão!
Passo 4
Agora podemos continuar para obtermos quem é a altura mínima.
Para isto, temos que obter uma equação . Lembrando do Passo 2, temos:
Só que . Logo,
Para que possamos calcular quem é quando (o valor de ), temos antes que descobrir . E para isto, basta aplicarmos a condição de que quando . Logo,
E por fim, a altura mínima será:
E assim finalizamos a questão!