Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 7.Problemas - Ex. 112
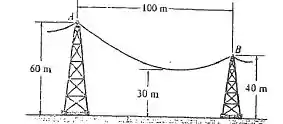
O cabo de transmissão de energia tem um peso por unidade de comprimento de . Se o ponto mais baixo do cabo precisa estar pelo menos acima do solo, determine a tração máxima desenvolvida no cabo e o comprimento do cabo entre e .
Passo 1
O problema quer que a gente encontre a tração máxima no cabo e comprimento do cabo entre e .
Vamos começar fazendo um esqueminha, assim:
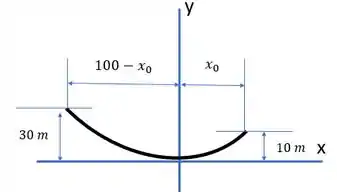
Onde o carregamento pode ser descrito como:
Passo 2
Nós notamos que na figura do problema, é o ponto mais baixo do cabo.
Escolhemos posicionar nosso cabo de forma muito estratégica em relação ao eixos coordenados. Para essa situação, que a gente fez no diagrama, esse referencial, temos que em e a gente tem a inclinação do cabo
E temos também que em , nosso eixo vale . Para essa situação e como temos um cabo que suporta apenas o seu peso, valem as relações:
Onde é a componente horizontal da tração no cabo em todos os pontos e é o peso do nosso cabo. Substituindo o que o enunciado deu, ficamos com:
Agora, testamos a função em pontos conhecidos, que são quando e quando :
Calculando essa duas equações como um sistema de duas variáveis, encontramos:
Passo 3
A maior tensão irá acontecer em , porque a gente percebe que ele tem o maior ângulo, então vamos calcular o ângulo dele. A coordenada dele é
Lembra, a derivada é a tangente do ângulo em um ponto de uma função. Nossa derivada é
Aí o ângulo no ponto é:
Logo, a tração máxima será:
Passo 4
Vamos agora pegar o diagrama do corpo livre de um pedacinho da corda, assim:
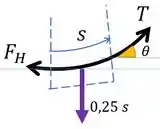
Lembrando que é a compoente horizontal da força de tração em qualquer lugar. Aí ela aparece ali onde .
E usamos as equações de equilíbrio nos dois eixos:
Eliminando , aparece a tangente que faz a aparecer a derivada:
Então igualamos a equação derivada:
Assim encontramos:
O comprimento do cabo é dado por: