Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.3 - Ex. 3
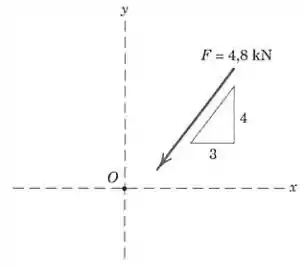
A inclinação da força de está especificada como mostrado na figura. Expresse como um vetor, em termos dos vetores unitários e .
Passo 1
O triângulo da figura é o famoso triângulo retângulo de catetos e e hipotenusa . Podemos usá-lo para determinar as componentes em e do vetor .
Se liga nessa dica para você entender melhor a decomposição
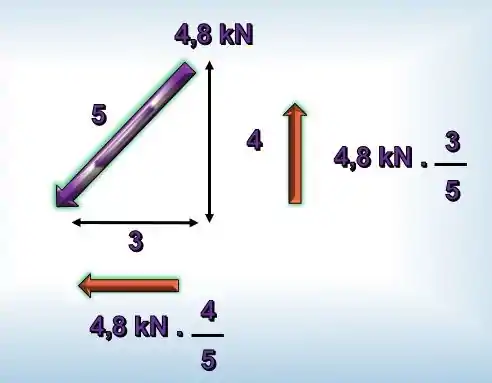
Só observem que a força é para baixo, então é negativa
E portanto,
Resposta
Exercícios de Livros Relacionados
Determine os componentes da força de 2k N ao longo dos eixos oblíquos a e b . Determine as projeções de F sobre os eixos a e b .
Determine os componentes escalares R a e R b da força R ao longo dos eixos não retangulares a e b . Determine também a projeção ortogonal P a de R sobre o eixo a .
A razão entre a força de sustentação L e a força de arraste D , para um aerofólio simples, é L / D = 10 . Se a força de sustentação em uma seção curta do aerofólio vale 200N , calcule o módulo da forç
Deseja-se remover o pino da madeira pela aplicação de uma força ao longo de seu eixo horizontal. Um obstáculo A impede um acesso direto, de modo que duas forças, uma de 1,6k N e a outra P , são aplica
Em que ângulo θ uma força de 800N deve ser aplicada para que a resultante R das duas forças tenha um módulo de 2000N ? Para esta condição, determine o ângulo β entre R e a vertical.