Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.3 - Ex. 6

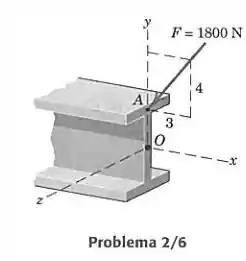
A força F de 1800 N é aplicada à extremidade da viga em H. Expresse F como um vetor, usando os vetores unitários i e j.

Passo 1

Os vetores i e j são vetores de tamanho de 1 unidade de grandeza que representam as direções e , respectivamente. Então se temos uma força de módulo na direção , por exemplo, o vetor força fica completamente definido quando o representamos como , pois agora adicionamos o sentido e a direção dele. O que temos que fazer então é decompor a força em componentes nas direções e , e então multiplicar as componentes por e .

Passo 2

A angulação da força no plano em relação ao eixo é dada pelas distâncias da figura. Temos um triângulo retângulo de catetos 3 e 4, então a hipotenusa vale:

Então fica definido o ângulo entre a força e a direção .

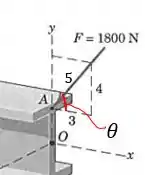
A compontente da força será vezes o cosseno do ângulo, só que negativo, pois aponta no sentido contrário a :

A componente será vezes o seno, e também é negativa:

Então temos nosso vetor :

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A linha de ação da força F de 9,6k N passa pelos pontos A e B , como mostrado na figura. Determine os componentes escalares x e y de F .

Duas forças são aplicadas ao suporte de construção, como mostrado. Determine o ângulo θ que faz com que a resultante das duas forças seja vertical. Determine o módulo R da resultante.

A inclinação da força F de 4,8k N está especificada como mostrado na figura. Expresse F como um vetor, em termos dos vetores unitáriosi e j .

A força F em um módulo de 800N . Expresse F como um vetor, em termos dos vetores unitáriosi e j . Identifique os componentes escalares de F em x e y .

No projeto de um mecanismo de controle é determinado que a barra A B transmite uma força P de 260N à manivela B C . Determine os componentes escalares x e y de P .