Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 180

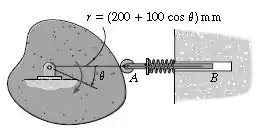
No instante θ = 30 ° , a came gira com uma velocidade angular no sentido horário de θ ˙ = 5   r a d / s   e aceleração angular de θ ¨ = 6   r a d / s 2 . Determine as intensidades da velocidade e aceleração da barra seguidora A B neste instante. A superfície da came tem umm formato da limaçon (caracol de Pacal) definida por r = 200 + 100 cos ⁡ θ m m .

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

O enunciado nos pede as intensidades da velocidade e aceleração da barra seguidora A B no instante descrito no enunciado.

Nos é dada a equação da posição:

r = 200 + 100 cos ⁡ θ

Vamos derivar essa equação dos dois lados:

d d t ( r ) = d d t ( 200 + 100 cos ⁡ θ )

d r d t = - 100 sin ⁡ θ d θ d t

r ˙ = - 1 00 sin ⁡ θ θ ˙

A segunda derivada é dada por:

d d t ( r ˙ ) = d d t ( - 100 sin ⁡ θ θ ˙ )

Note que agora temos que aplicar a regra do produto na derivação pois temos sin ⁡ θ multiplicando θ ˙ .

A regra do produto é aplicada quando é necessário fazer a derivada do produto de equações.

Logo:

d r ˙ d t = - 1 00 cos ⁡ θ d θ d t θ ˙ + sin ⁡ θ d θ ˙ d t

r ¨ = - 1 00 cos ⁡ θ θ ˙ θ ˙ + sin ⁡ θ θ ¨

r ¨ = - 1 00 cos ⁡ θ θ ˙ 2 + sin ⁡ θ θ ¨

Passo 2

Vamos agora aplicar θ = 30 ° , θ ˙ = 5   r a d / s e θ ¨ = 6   r a d / s 2 :

r θ = 30 ° = 200 + 100 cos ⁡ 30 °

r θ = 30 ° = 2 86,60   m m

r ˙ θ = 30 ° = - 1 00 sin ⁡ 30 ° ( 5 )

r ˙ θ = 30 ° = - 250   m m / s

r ¨ θ = 30 ° = - 100 cos ⁡ 30 ° 5 2 + sin ⁡ 30 ° 6

r ¨ θ = 30 ° = - 2 4 65,06   m m / s 2

Passo 3

Agora pensa comigo... As componentes radiais da velocidade e da aceleração, nos dão exatamente as magnitudes para a barra A B . Portanto:

v A B = v r = r ˙

v A B = - 250   m m / s

E:

a A B = a r = r ¨ - r θ ˙ 2

a A B = - 24 56,06 - 286,6 5 2

a A B = - 96 30   m m / s 2

Resposta

v A B = - 250   m m / s

a A B = - 96 30   m m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Solucione o Problema 12.190 se a partícula tiver uma aceleração angular de θ ¨ = 5r a d / s 2 quando θ ˙ = 4r a d / s a θ = π / 2r a d .
A superfície parcial da came é uma espiral logarítmica r = 40 e 0,05 θm m , onde θ é dado em radianos. Se a came gira a uma velocidade angular constante de θ ˙ = 4r a d / s , determine as intensidades
A fenda do braço A B impulsiona o pino C pela fenda espiral descrita pela equação r = 1,5 θ m , onde θ é dado em radianos. Se p braço sai do repouso quando θ = 60 ° e é impulsionado a uma velocidade a
Determine a velocidade escalar do bloco A se a extremidade B da corda é puxada para baixo com uma velocidade escalar de 1,5m / s .
Determine a velocidade escalar do bloco A se a extremidade B da corda é puxada para baixo com uma velocidade escalar de 6m / s .