Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 187
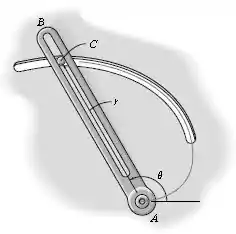
A fenda do braço impulsiona o pino pela fenda espiral descrita pela equação , onde é dado em radianos. Se p braço sai do repouso quando e é impulsionado a uma velocidade angular de , onde é dado em segundos, determine as componentes radiais e transversais da velocidade e aceleração do pino quando .
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
O enunciado nos pede as componentes radiais e transversais da velocidade e aceleração do pino quando .
Do enunciado, temos que:
Integrando, temos:
Como , temos que:
Passo 2
Quando , temos:
E:
Queremos:
E:
Passo 3
Vamos às analises:
Como , temos que:
E:
Passo 4
Sabemos que:
Passo 5
Para a aceleração, teremos que a componente é:
A componente é dada por:
Resposta
Exercícios de Livros Relacionados
2/135) Um carro P se desloca ao longo de uma estrada reta com uma velocidade constante v = 100 k m / h . No instante em que o ângulo θ = 60 ° , determine os valores de r ' em m / s e θ ' em graus/s .
2/145) Um mecanismo interno é usado para manter uma velocidade angular constante Ω = 0,05r a d / s em torno do eixo z da espaçonave enquanto as hastes telecópicas são prolongadas a uma taxa constante
2/142) Enquanto o cilindro hidráulico gira em torno de O , o comprimento exposto l da haste do pistão P é controlado pela ação da pressão do óleo no cilindro . Se o cilindro gira na taxaconstante θ '
2/137) O movimento do bloco deslizante P na ranhura radial rotativa é controlado pelo parafuso como mostrado . Para o instante representado θ ' = 0,1 r a d / s , θ " = - 0,4 r a d / s 2 e r = 300 m m
2/139) A haste O A B gira em torno do ponto O , enquanto a seção A B simultameamente prolonga-se de dentro da seção O A . Determine a velocidade e a aceleração do centro B da polia para as seguintes c