Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.4 - Ex. 94

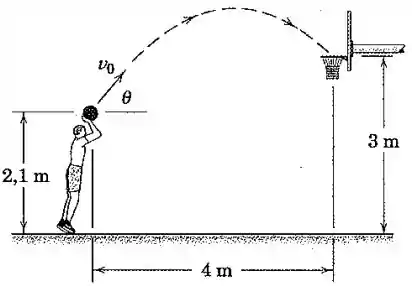
O jogador de basquete gosta de arremessar seu lance livre em um ângulo θ = 50 ° com a horizontal como mostrado. Que velocidade inicial v 0 fará com que a bola passe através do centro do aro?

Passo 1

Pessoal, como temos todas as dimensões de x e y no lançamento e no alvo, será bastante útil desenvolvermos a equação da trajetória, que nos dá justamente y em função de x .

Começamos pela seguinte equação do movimento horizontal:

x = x 0 + v x t = x 0 + v 0 cos ⁡ θ t

t = x - x 0 v 0 cos ⁡ θ

Agora, a gente escreve a seguinte equação do movimento vertical:

y = y 0 + v 0 y t - 1 2 g t 2 = y 0 + v 0   s e n   θ t - 1 2 g t 2

Só resta substituir a expressão de t já encontrada:

y = y 0 + v 0   s e n   θ x - x 0 v 0 cos ⁡ θ - 1 2 g x - x 0 v 0 cos ⁡ θ 2

y = y 0 + t g   θ x - x 0 - g sec 2 ⁡ θ 2 v 0 2 x - x 0 2

Então essa é a equação da trajetória de um projétil lançado da posição ( x 0 ,   y 0 ) com velocidade v 0 e fazendo um ângulo θ com a horizontal, beleza?

Passo 2

Agora só nos resta substituir os dados que temos na equação para encontrar v 0 . Considerando o pé do jogador como a origem do nosso sistema de coordenadas, teremos x 0 = 0   m e y 0 = 2,1   m . Além disso, θ = 50 ° e g = 9,8   m / s 2 . Escolheremos o ponto x ,   y = ( 4   m ,   3   m ) para aplicar, pois é onde fica o centro do aro:

y = y 0 + t g   θ x - x 0 - g sec 2 ⁡ θ 2 v 0 2 x - x 0 2

3 = 2,1 + t g   50 ° 4 - 0 - 9,8 sec 2 ⁡ 50 ° 2 v 0 2 4 - 0 2

3 = 2,1 + 4,77 - 189,7 v 0 2

189,7 v 0 2 = 3,87

v 0 = 7   m / s

Resposta

v 0 = 7   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um jogador de ferradura lança a ferradura em A com uma velocidade inicial v 0 = 11m / s . Determine a faixa para o ângulo de lançamento θ para o qual a ferradura baterá na estaca vertical de 350m m .
Um menino lança uma bola para cima com uma velocidade v 0 = 12m / s . O vento transmite uma aceleração horizontal de 0,4m / s 2 para a esquerda. Em que ângulo θ a bola deve ser atirada para que esta r
A velocidade de disparo de um fuzil de longo alcance em A é u = 400m / s . Determine os dois ângulos de elevação θ , que permitirão ao projétil acertar a montanha no alvo B .
Um projétil é lançado a partir do ponto A com uma velocidade inicial v 0 = 30m / s . Determine o valor mínimo do ângulo de lançamento α com o qual o projétil cairá no ponto B .