Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.4 - Ex. 86
Um menino lança uma bola para cima com uma velocidade . O vento transmite uma aceleração horizontal de para a esquerda. Em que ângulo a bola deve ser atirada para que esta retorne ao ponto de lançamento? Admita que o vento não afeta o movimento vertical.
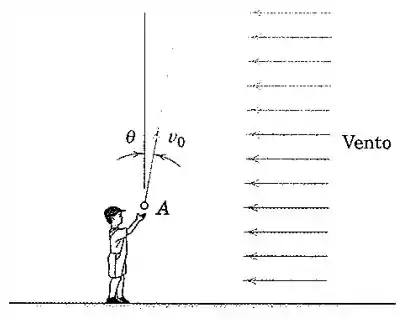
Passo 1
Perceba que o ângulo é medido em relação à vertical, não à horizontal. Ou seja,
Analisando o movimento horizontal, temos:
Considerando o instante em que a bola retorna ao ponto , teremos , certo?
Passo 2
Agora analisamos o movimento vertical:
Vamos substituir , que é o tempo para que a bola retorne ao ponto , e então :
Dividimos tudo por
Resposta
Exercícios de Livros Relacionados
Se o jogador de tênis dá o saque horizontalmente ( θ = 0 ) , calcule sua velocidade v se o centro da bola transpõe a rede de 0,9m por 150m m . Encontre também a distância s a partir da rede até o pont
Um projétil é disparado com uma velocidade u na entrada A de um túnel horizontal de comprimento L e altura H . Determine o valor mínimo de u e o valor correspondente do ângulo θ para o qual o projétil
Um projétil é disparado com uma velocidade u perpendicular ao declive, que está inclinado de um ângulo θ com a horizontal. Derive uma expressão para a distância R até o ponto de impacto.
Determine a localização h do ponto em direção ao qual o arremessador deve lançar a bola de modo que ela atinja a mão do receptor. A bola é lançada com uma velocidade de 40m / s .
Para atender a critérios de projeto, pequenas esferas de rolamento devem saltar através de uma abertura de tamanho limitado no topo de sua trajetória após repercutir a partir de uma chapa inerte como