Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.4 - Ex. 96
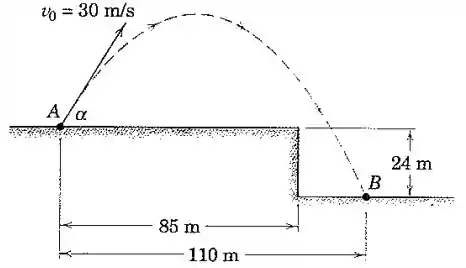
Um projétil é lançado a partir do ponto com uma velocidade inicial . Determine o valor mínimo do ângulo de lançamento com o qual o projétil cairá no ponto .
Passo 1
Como a gente tem todas as dimensões do problema e não precisamos de saber nada a respeito do tempo, será útil construirmos a equação da trajetória de um projétil desse tipo.
Começamos pela seguinte equação do movimento horizontal:
Agora, a gente escreve a seguinte equação do movimento vertical:
Só resta substituir a expressão de já encontrada:
Então essa é a equação da trajetória de um projétil lançado da posição com velocidade e fazendo um ângulo com a horizontal, beleza?
Passo 2
Nessa situação da figura, podemos colocar , (coordenadas do ponto ), e . Também já vamos substituir e , que são as coordenadas do ponto :
Lembrando que , temos:
Passo 3
No passo anterior, encontramos dois valores de para os quais o projétil chega em . Porém, não temos certeza se o projétil consegue ultrapassar aquela quina em . Pra testar isso, vamos novamente usar a equação da trajetória, substituindo esse valor de e cada valor de ângulo obtido:
Como , o projétil acerta o chão antes do degrau, então o valor de não pode ser a solução.
Agora testemos o valor de :
Agora sim temos , e portanto, o valor mínimo é: