Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.4 - Ex. 91
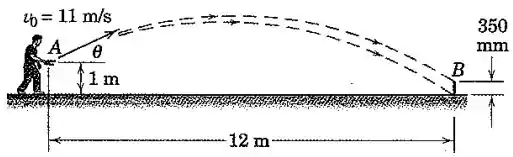
Um jogador de ferradura lança a ferradura em com uma velocidade inicial . Determine a faixa para o ângulo de lançamento para o qual a ferradura baterá na estaca vertical de .
Passo 1
Pessoal, para que a ferradura acerte a estaca, precisamos que, quando , tenhamos . Então, será útil construirmos a equação da trajetória de um projétil desse tipo.
Começamos pela seguinte equação do movimento horizontal:
Agora, a gente escreve a seguinte equação do movimento vertical:
Só resta substituir a expressão de já encontrada:
Então essa é a equação da trajetória de um projétil lançado da posição com velocidade e fazendo um ângulo com a horizontal, beleza?
Passo 2
Nessa situação da ferradura, podemos colocar , , e . Também já vamos substituir , para ter uma expressão para em função apenas de quando a ferradura cruza a vertical da estaca:
Para que a ferradura acerte a estaca, devemos ter . Então:
Lembrando que , temos:
Isso nos dá duas inequações, que devem ser simultaneamente satisfeitas:
Passo 3
Olhe para a primeira inequação:
Temos que achar as raízes da equação correspondente:
Como o sinal do termo quadrático na inequação era negativo, teremos aquela expressão maior do que zero quando:
Então sabemos que deve estar necessariamente nessa região, mas ainda precisamos fazer a intersecção com a solução da outra inequação.
Passo 4
Vamos para a segunda inequação:
Agora a gente resolve a equação correspondente:
Porém, na inequação , temos o termo quadrático positivo, e portanto, para que a expressão toda seja maior do que zero, precisamos que:
Agora, fazendo a intersecção com a solução obtida anteriormente , resultará em dois intervalos: