Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 44
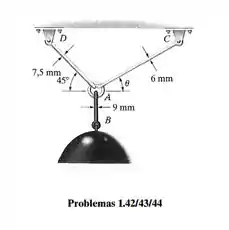
A luminária de é sustentada por três hastes de aço interligadas por um anel em . Determine o ângulo de orientação de de modo que a tensão normal média na haste seja duas vezes a tensão normal média na haste . Qual é a intensidade da tensão em cada haste? O diâmetro de cada haste é dado na figura.
Passo 1
Fala aí galerinha do responde aí, vamos garantir aquele notão em Resmat?
Sabemos que a tensão é dada pela força dividida pela área, ou seja, temos que calcular a força em cada haste e dividir pelas respectivas áreas. O DCL fica:
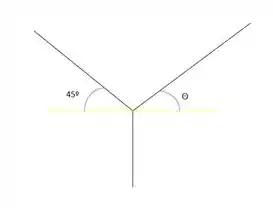
Primeiramente, vamos decompor as forças e aplicar as equações de equilíbrio:
O problema nos dá a seguinte condição:
Como a tensão média é dada pela divisão entre a força e a área da seção reta, teremos:
Colocando uma força em evidência...
Beleza, agora é só calcular a área desses cabos...
Onde:
Repara que eu não precisei alterar a unidade para metros, pois como na equação vai ficar uma área dividida pela outra, a unidade vai acabar cancelando, por isso, não precisamos converter :)
Assim:
Temos um sistema de 3 equações e 3 incógnitas. Sabemos que é o peso da luminária:
Passo 2
Sistema montado, agora é só resolver. Uma dica aqui é usar o método da substituição, pois a gente tá trabalhando com senos e cossenos e fazer por escalonamento pode ser bem mais trabalhoso.
Substituindo a eq. 3, na eq. 1:
O que nos dá:
Substituindo a equação 3, na equação 2 e usando o valor de :
E por último:
A gente substitui:
Passo 3
Agora, vamos calcular a última área:
Lembrando que as outras áreas são:
Por fim, basta fazer a força sobre a área: