Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 49

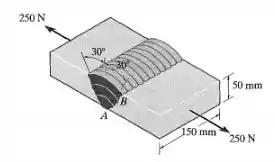
A junta de topo quadrada aberta é usada para transmitir uma força de 250 N e uma placa a outra. Determine as componentes da tensão de cisalhamento média e da tensão normal média que essa carga cria na face da solda, seção AB.

Passo 1

Primeiramente, vamos vizualisar o DCL:

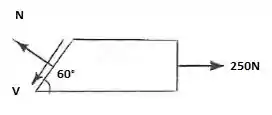
Decompondo-se as forças em x e y e fazendo o somatório de forças, ficamos com:

∑ F x = 0 → V c o s 60 ° - N c o s 30 ° + 250 = 0

∑ F y = 0 → - V s e n 60 ° + N s e n 30 ° = 0

Note que temos um sistema com 2 equações e 2 incógnitas. Resolvendo o sistema simples, teremos:

N = 216,506 N

V = 125 N

Passo 2

Agora, devemos calcular a área para então acharmos as tensões. Esta será o produto da largura de 150mm pela distância do plano inclinado:

A = 150 × 50 s e n ( 60 ° ) = 8660,25 m m ²

Passo 3

Com as forças e a área, podemos calcular as tensões:

σ = N A = 216,506 8660,25 = 0,025 M P a

τ = V A = 125 8660,25 = 0,0144 M P a

Resposta

σ = 0,025 M P a

τ = 0,0144 M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O corpo de prova falhou no ensaio de tração a um ângulo de 52° sob uma carga axial de 100 kN. Se o diâmetro do corpo de prova for 12 mm, determine a tensão de cisalhamento média e a tensão normal médi
A junta está submetida a uma força axial de 5k N . Determine a tensão normal média que age nas seções A B e B C . Considere que o elemento é liso e tem 50m m de espessura.
A prancha de madeira está sujeita a uma força de tração de 425N . Determine a tensão de cisalhamento média e a tensão normal média desenvolvidas nas fibras da madeira orientadas ao longo da seção a -
Os dois elementos de aço estão interligados por uma solda de topo angular de 60°. Determine a tensão de cisalhamento média e a tensão normal média suportada no plano da solda.