Durante uma corrida, o pé de um homem com massa é submetido momentaneamente a uma força equivalente a vezes o seu peso. Determine a tensão normal média desenvolvida na tíbia da perna desse homem na seção média . A seção transversal pode ser considerada circular, com diâmetro externo de e diâmetro interno de . Considere que a fíbula não está suportando nenhuma carga.
Passo 1
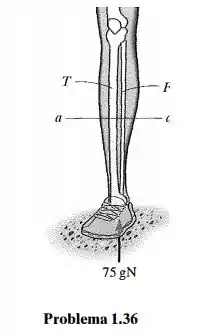
Fala aí galera, partiu tirar 10 em Resmat? Primeiro, vamos compreender o que esse moço quer da gente. Temos o pé de um homem, e tem uma hora que esse pé recebe uma força de 5 vezes o peso desse homem. Então ele recebe
Aí mais acima desse pé, tem a seção . Ele quer saber a tensão normal média nessa seção. Vamos lembrar da fórmilinha dessa tensão:
Onde é a força aplicada na seção. A gente acabou de ver que ela vale no pé. A perna dele vai ser tipo uma coluna. Essa força vai ser aplicada no pé e transmitida até . Então tá tranquilo essa parte. Só nos falta achar a área da seção.
Então, na real, esse problema é muito parecido com os outros problemas onde a gente tinha uma coluna com uma tentão axial, ok? Essa parada toda do osso é só para confundir haha
Passo 2
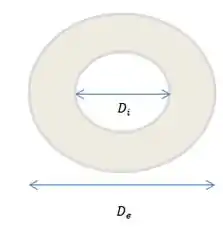
Vamos determinar a área. A seção transversal do osso pode ser considerada circular com um furo no centro, algo tipo assim:
Passo 3
Logo, a tensão normal será dada por:
Se liguem sempre nas unidades.