Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 46
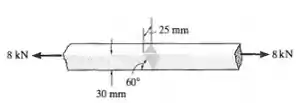
Os dois elementos de aço estão interligados por uma solda de topo angular de 60°. Determine a tensão de cisalhamento média e a tensão normal média suportada no plano da solda.
Passo 1
Primeiramente, devemos decompor as forças em uma componente tangencial a seção e uma normal a seção:
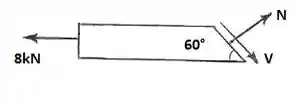
Logo, temos que:
= 8
Podemos ver que temos um sistema com 2 equações e 2 incógnitas, resolvendo o sistema, teremos:
Passo 2
Agora, devemos calcular a área da seção transversal inclinada. Esta será o produto da largura de 25mm pelo plano inclinado da seção:
=
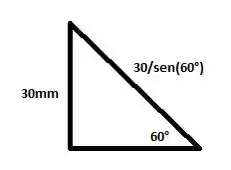
Passo 3
Calculando as tensões:
Resposta
Exercícios de Livros Relacionados
O raio do pedestal é definido por r=( 0,5 ⋅ e - 0.008 y 2 )m , onde y é dado em metros. Se o material tiver densidade de 2,5M g / m 3 , determine a tensão normal média no apoio.
A área da seção transversal da barra é 400 ⋅ 10 - 6 m 2 . Se ela estiver sujeita a uma carga axial distribuída uniformemente ao longo de seu comprimento e a duas cargas concentradas como mostra a figu
A barra uniforme com área da seção transversal A e massa por unidade de comprimento m está apoiada por um pino em seu centro. Se ela girar no plano horizontal a uma velocidade angular constante ω , de
A área da seção transversal da barra é 400 ⋅ 10 - 6 m 2 . Se ela estiver sujeita a uma carga axial distribuída uniformemente ao longo de seu comprimento e a duas cargas concentradas como mostra a figu
O pedestal suporta uma carga P em seu centro. Se a densidade de massa do material for ρ , determine a dimensão radial r em função de z de modo que a tensão normal média no pedestal permaneça constante