Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 91
A lança é suportada pelo cabo do guincho com diâmetro de com tensão normal admissível . Se a lança tiver de levantar lentamente uma carga de , de até , determine o menor diâmetro do cabo com aproximação de múltiplos de . O comprimento da lança é . Despreze o tamanho do guincho e considere .
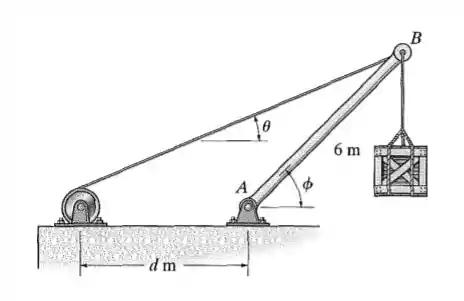
Passo 1
Falaaa! Bora comçar!
Queremos o diâmetro no cabo, certo? Como a gente tem a tensão admissível, vamos precisar achar a força no cabo. Maaas a gente tem duas situações limite de . O que faremos?
Para poupar esforços, a gente pode achar em função de e ver qual dos dois casos resulta em um esforço maior, ok? Já que a gente quer dimensionar ele, precisamos olhar as situações extremas.
Para facilitar nossa vida, vamos definir alguns ângulos aqui:
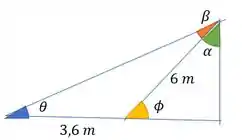
Aí a gente pode começar fazendo um DCL da nossa situação:
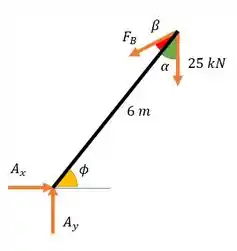
Passo 2
Vamos achar ! A gente pode fazer o somatório de momentos em , com sentido anti-horário como positivo:
A gente consegue reescrever esse denominador usando uma identidade trigonométrica:
Passo 3
Vamos achar e em função de . Olhando nosso desenho:
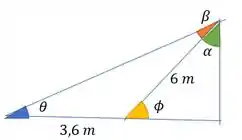
Podemos usar a Lei de Senos no triângulo da esquerda:
E pelos ângulos internos do triângulo a gente acha:
Vamos substituir isso em , e testar e :
Fazendo para : (jogando na calculadora)
Fazendo para :
Daí a gente tira que a situação que exige mais do cabo (onde o esforço nele é maior) é . Então vamos usar
Passo 4
Podemos achar o diâmetro através da fórmulinha da tensão normal média. Ela é assim:
Vamos isolar :
Se a gente fizer e a gente acha o diâmetro mínimo para aguentar essa tensão no cabo.
Aproximando para um múltiplo de 5 vamos obter