Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.3 - Ex. 4
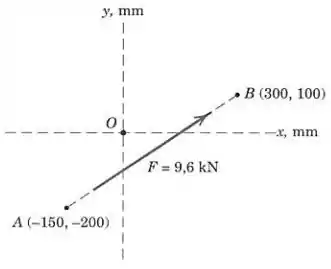
A linha de ação da força de passa pelos pontos e , como mostrado na figura. Determine os componentes escalares e de .
Passo 1
O vetor está na mesma direção e sentido de um vetor que vai de até , calculado assim:
Outro modo de escrever o vetor é assim:
Passo 2
Agora, lembre-se de que, quando dois vetores têm mesma direção e mesmo sentido, então um é múltiplo escalar do outro. Ou seja, existe um número tal que:
Com isso, obtemos duas equações:
Igualando , temos:
Passo 3
Beleza, agora só falta usar a equação do módulo:
E então:
Resposta
Exercícios de Livros Relacionados
O módulo da força F é 6 00N . Expresse F como um vetor, em termos dos vetores unitáriosi e j . Identifique os componentes escalares e vetoriais de F .
Os dois elementos estruturais, um sob tração e o outro sob compressão, exercem as forças indicadas no nó O . Determine o módulo da resultante R das duas forças e o ângulo θ que R faz com o eixo x posi
Um cabo esticado entre os suportes fixos A e B está sob uma tração T de 900N . Usando os vetores unitários i e j expresse a tração como um vetor; primeiramente como uma força T A atuando em A e, em se
Determine o módulo F s da força trativa atuando na mola, para que a resultante de F s e de F seja uma força vertical. Determine o módulo R dessa força resultante vertical.
Para o mecanismo do Prob. 2/9, determine os componentes escalares P t e P n de P , que são tangente e normal, respectivamente, à manivela B C .