Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.3 - Ex. 10

Para o mecanismo do Prob. 2/9, determine os componentes escalares e de , que são tangente e normal, respectivamente, à manivela .

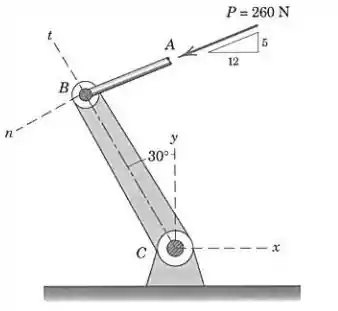
Passo 1

Pessoal, a força pode ser decomposta nas suas componentes tangente e normal conforme mostra a figura a seguir:

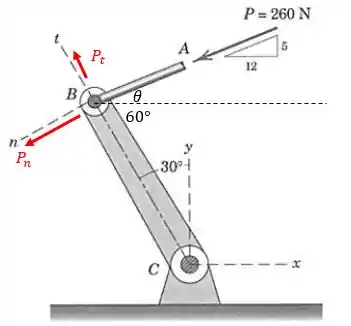
Para facilitar a nossa análise, vamos colocar o eixo da nossa composição em cima do eixo e e vamos dar uma leve “girada” para deixar o nosso eixo perpendicular para nós:

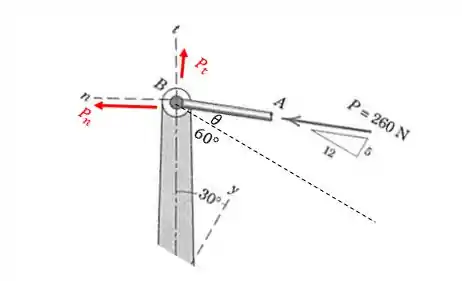
Agora sim facilitou a visualização, não é?

Repare que para encontrar as componentes que a gente quer encontrar é interessante a gente procurar quem é o ângulo (o que a gente vai fazer no passo 2).

Depois do âgulo encontrado, há de concordar comigo que dái, para obter as componentes das forças, bastará a gente olhar para o triângulo formado entre a manivela e o nosso eixo (triângulo de ângulo :

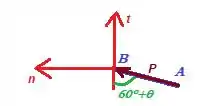
O que a gente vai fazer no passo 3 é justamente encontrar as componentes que já poderam ser encontradas assim:

Passo 2

O ângulo pode ser calculado por meio do triângulo retângulo mostrado na figura do triângulo dado:

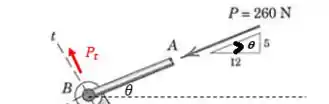
Então...

Passo 3

Encontrado o valor de é só aplicar as equações que a gente definiu no passo 1 para encontrar as componentes .

Logo, temos:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

2.36. Se Φ = 30 ° e F 2 = 3k N , determine a intensidade da força resultante que atua sobre a chapa e sua direção θ, medida no sentido horário a partir do eixo x positivo.

2.41. Determine a intensidade e a direção θ de F B , de modo que a força resultante seja direcionada ao longo do eixo y positivo e tenha uma intensidade de 1500N .

2.40. Determine a intensidade e a direção, medida no sentido anti-horário a partir do eixo x positivo, da força resultante das três forças que atuam sobre o anel A. Considere F 1 = 500N e θ = 20 ° .

2.39. Determine a intensidade de F 1 e sua direção θ, de modo que a força resultante seja direcionada verticalmente para cima e tenha a intensidade de 800N .

2.43. Se Φ = 30 ° e F 1 = 1,25k N , determine a intensidade da força resultante que atua sobre o suporte e sua direção, medida no sentido horário a partir do eixo x positivo.