Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.6 - Ex. 82
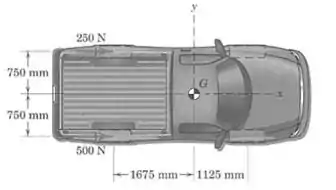
Sob condições não uniformes e escorregadias da estrada, as duas forças mostradas são exercidas sobre as duas rodas de tração traseiras da caminhonete, que tem um diferencial traseiro que limita derrapagens. Determine a interseção com o eixo da resultante desse sistema de forças.
Passo 1
Vamos escrever as duas forças em forma vetorial:
O vetor (força resultante) pode ser calculado apenas somando essas duas forças:
Passo 2
Agora temos que definir a posição em que essa força resultante atua. A posição não altera a força em si, mas altera o momento total dela.
A nossa ideia aqui é preservar o momento do estado inicial (o que está na figura do enunciado), então vamos calcular em relação ao ponto :
Para que a força produza esse mesmo momento, a posição dela no eixo deve satisfazer essa equação aqui:
Existe um perigo nessa conta: nós usamos o módulo, então precisamos verificar nosso resultado de acordo com as convenções que escolhemos.
O nosso momento total era positivo, então tínhamos rotação no sentido anti-horário. Para isso é preciso que a força esteja abaixo do ponto no eixo , e portanto a altura em que a nossa força age deve ser:
Resposta
A resultante age na altura .