Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.4 - Ex. 45
Determine a coordenada y do centroide da área sombreada.
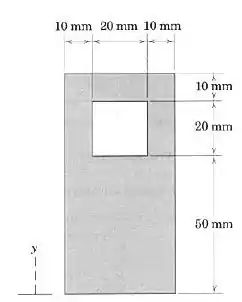
Passo 1
Sabendo que aa equação para encontrar o centro de massa é dado por:
Dessa maneira, vamos primeiro encontrar os centros de cada parte.
Passo 2
Mas antes vamos separar cada componente, de tal modo que:
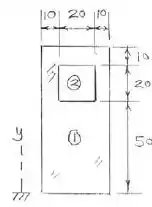
Pronto! Escolhido os componentes vamos montar uma tabela com parte
Passo 3
No primeiro componente, vemos que a área é dada 40mm de comprimento e 80mm de altura, logo o fica no meio da altura, portanto .
Já no segundo componente, na qual devemos subtrair da peça, vemos que a área corresponde a 20mm de comprimento e 20mm de altura.
Cuidado! Observe que o fica no meio da peça, no caso 20mm, mas devemos somar mais 40mm por causa que nossa origem está no início do objeto não no início da peça que iremos retirar.
Passo 4
Agora só basta substituir na equação que teremos nosso ponto: