Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 9.Problemas - Ex. 70
Localize o centro de massa para a montagem do compressor. As localizações dos centros de massa dos diversos componentes e suas massas são indicados e tabulados na figura. Quais são as reações verticais nos blocos e necessárias para suportar a plataforma?
Passo 1
O problema quer que a gente encontre o centro de massa do compressor e das reações nos verticais nos pontos e .
Vamos relembrar que o peso de um corpo extenso atua como se atuasse diretamente no centro de massa do corpo. Aí a gente usa o momento para calcular as forças de reações, assim:
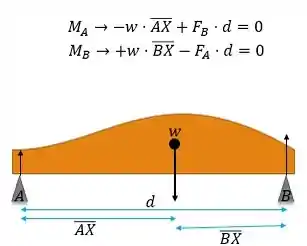
Passo 2
Então vamos vamos fazer uma tabela com as informações para calcular o centro de massa:
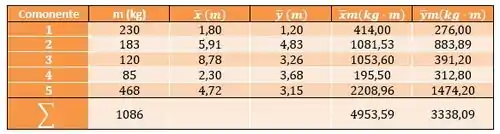
Agora, já com essas informações calculadas, vamos obter os centros de massa nos eixos e :
Passo 3
Usando o momento a gente pode calcular as reações nos blocos e , vamos lá:
Primeiro vamos calcular o momento considerarando o bloco como eixo de rotação.
Agora considerando o bloco como eixo de rotação.