Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 9.Problemas - Ex. 59
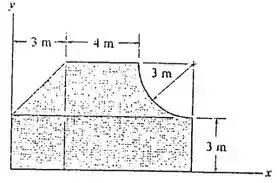
Localize o centroide da área composta.
Passo 1
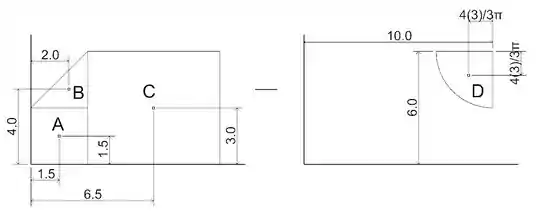
Nesse exercício vamos precisar dividir nossa área em partes mais simples, vou usar um quadrado, um triângulo, um retângulo e de círculo.
Utilizando uma tabela de centroides encontramos as fórmulas para cada formato desses e identificamos seus centroides, onde do retângulo e do quadrado está no seu centro e do triângulo a do seu lado maior e para o quarto de círculo usamos .
Faremos então :
Passo 2
Lembrando que a área do quarto de círculo é:
Vamos agora montar uma tabela com nossos dados e encontrar os somatórios:
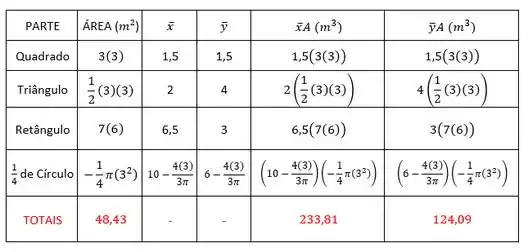
Ficamos com:
Logo,
Resposta
Exercícios de Livros Relacionados
Uma estante é feita de chapa de aço laminado e possui a seção transversal mostrada na figura .Determine a localização (x, y) do centroide da seção transversal. As dimensões são indicadas para cada seg
Localize o centroide (x, y) da seção transversal do elemento.
Determine a localização (x, y, z) do centroide do elemento homogêneo.
Localize o centro de massa do bloco. Os materiais 1, 2 e 3 possuem densidades de 2,70M g / m ³ ³, 5,70M g / m ³ ³ e 7,80M g / m ³ ³ , respectivamente.
Localize o centroide y da seção transversal da viga.