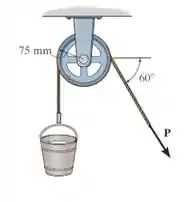
A polia é suportada por um pino de de diâmetro. Se a polia se ajusta livremente no pino, determine a maior força que pode ser aplicada à corda e ainda baixar o balde. O balde tem uma massa de e o coeficiente de atrito estático entre a polia e o pino é . Despreze a massa da polia e assuma que o cabo não desliza na polia.

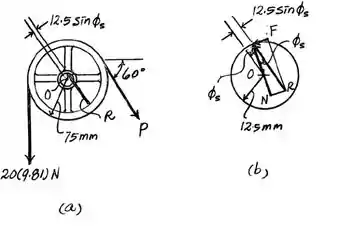
Pra começar essa questão vamos analisar as forças atuando na roldana. No diagrama letra podemos decompor a força nas suas componentes horizontal () e vertical (). O somatório das forças verticais e horizontais que atuam no corpo em equilíbrio deve ser igual a zero. Assim, assumindo que a direção positiva é para direita, temos:

Agora, adotando como referencial positivo a direção para cima, temos:

Uma vez que encontramos as componentes vertical e horizontal de , podemos calcular o módulo dele. Assim,

Vamos agora usar nossa velha amiga geometria plana no diagrama de corpo livre da letra . Através do triângulo formado por podemos encontrar o valor para o ângulo . Vamos calculá-lo!

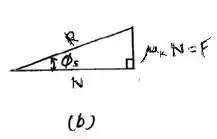
Assim, sabemos que o braço pro momento de no ponto passa a ser . Usando esses resultados, vamos escrever a equação do momento em relação ao ponto . O somatório de momentos para um sistema em equilíbrio, em relação a um ponto, deve ser igual a erro. Logo, assumindo com o sentido positivo anti-horário, temos:

Resolvendo essa equação e escolhendo uma raiz tal que , temos: