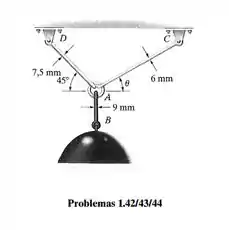
A luminária de é sustentada por três hastes de aço interligadas por um anel em . Determine qual das hastes está submetida à maior tensão normal média e calcule seu valor. Considere . O diâmetro de cada haste é dado na figura.

Fala aí galerinha do responde aí, bora pra outra questão.

Sabemos que a tensão da luminária é dada pelas três hastes e seu módulo pode ser dado pelo cálculo da força dividida pela área de cada uma das hastes, ou seja, temos que calcular a força em cada haste e dividir pelas respectivas áreas. O diagrama de corpo livre fica mais ou menos assim:

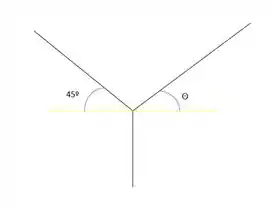
Primeiramente, vamos decompor as forças e aplicar as equações de equilíbrio:

Como temos em x duas hastes prendendo vindo uma de casa lado, faremos a soma da força da primeira haste com a segunda haste. Acontece que, se adotarmos positivo o x para o lado direito, então a outra haste em x terá um valor negativo. Além disso, precisamos achar a decomposição da força em x, já que as hastes estão em diagonal. Logo, teremos que:

Logo,

E essas são as nossas forças que influenciam no entendimento do eixo x. Agora, vamos realizar a análise das forças no eixo y. No eixo y, nós temos a influência de 3 forças: a foça da haste da direita e a da esquerda, que assim como em x, também têm suas decomposições em y, e a força peso, que puxa a luminária para baixo. Vamos adotar o sentido para cima como positivo. Sendo assim, teremos a força peso negativa e o seguinte somatório:

Temos um sistema de 2 equações e 2 incógnitas. Sabemos que é o peso da luminária e vale 30 graus, logo, resolvendo o sistema:

Resolvendo:

Logo, encontramos pra esse sistema o valor de: