Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas - Ex. 93
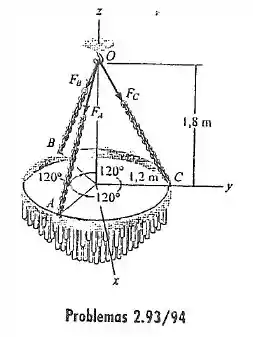
O lustre é sustentado por três corrente que são concorrentes no ponto . Se a força em cada corrente possui uma intensidade de , expresse cada força como um vetor cartesiano e determine a intensidade e os ângulos de direção coordenados da força resultante.
Passo 1
Fala! A gente quer a força resultante para esse caso e seus ângulos de direção.
Temos que determinar cada vetor força , e . Após isto, executaremos a soma das três forças e obtendo a força resultante.
Para determinar o vetor de uma força, a gente precisa multiplicar o módulo dessa força por um vetor unitário na direção e sentido da força.
Vamos trabalhar com o vetor de . O vetor na direção dele é o que sai de e vai para . Então podemos escrever esse vetor pela diferença de coordenadas entre esses pontos
Sendo
Para as coordenadas de A vamos precisar usar trigonometria. Pela figura, vemos que o segmento que passa pela origem e vai até A faz um ângulo de com o eixo e tem comprimento .
O que vamos fazer é projetar esse segmento em e em para achar essas coordenadas para . Como o ângulo está colado em , ele fica com cosseno:
Atenção que a coordenada é negativa, pela figura. Nosso ponto fica:
E o vetor fica:
Aí a força fica:
Passo 2
Determinando o vetor , vamos fazer algo parecido
Repara que está na parte negativa de e . A força fica:
Passo 3
Determinando o vetor : Ele vai ser mais simples porque conseguimos mais tranquilo as coordenadas de :
Isso porque o segmento entre ele e a origem está sobre o eixo . Aí o vetor na direção da força fica:
Aí a força fica:
Passo 4
Agora que possuímos todos os vetores definidos, podemos determinar força resultante somando-os.
Portanto, a força resultante conforme esperado aponta para baixo no sentido do eixo
Passo 5
Agora para determinar os ângulos do vetor resultante, aplicarmos a seguinte relação:
Aplicando arco cos, e substituindo os respectivos valores, temos: