Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 4.Problemas - Ex. 107
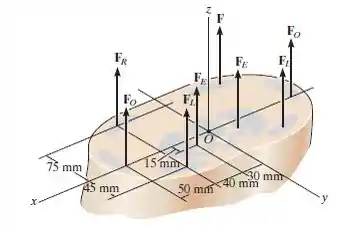
A figura mostra um modelo biomecânico da região lombar do tronco humano. As forças que agem nos quatro grupos de músculos consistem em para o reto, para o oblíquo, para o músculo grande dorsal e para o eretor da espinha. Esses carregamentos são simétricos em relação ao plano . Substitua esse sistema de forças paralelas por uma força e um momento binário equivalente agindo na espinha, no ponto . Expresse os resultados na forma de vetor cartesiano.
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
A ideia aqui é substituir as forças dadas no enunciado da questão por uma força resultante e por um momento , ambos em relação ao ponto .
Como todas as forças estão na direção positiva do eixo , basta somarmos todas as forças e indicarmos que estão na direção !
Já em relação ao momento, vamos analisar calmamente. Como todas as forças são paralelas ao eixo , não teremos momento resultante nesta direção.
Além disto, sabemos que as forças são simétricas em relação ao plano . Portanto, não há momento na direção . Então, o momento resultante será apenas na direção !
E como temos pares de forças, o momento será o dobro da soma dos momentos das forças , , e !
Então, vamos aos cálculos!
Passo 2
Primeiramente, vamos determinar a força resultante.
Aqui é bem tranquilo. Basta somarmos a intensidade de todos os vetores. Logo,
E assim finalizamos a primeira parte da questão!
Passo 3
Para finalizarmos, temos que calcular o momento em relação ao ponto . Como dissemos no Passo 1, basta calcularmos o momento relativo ao eixo . Logo,
Lembrem-se sempre de checar pela regra da mão direita o sinal do momento calculado!
E assim a gente finaliza a questão!
Resposta
A força resultante é
E o momento de binário é