Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 8.Problemas - Ex. 118
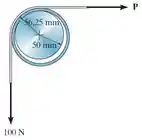
A luva encaixa-se livremente em torno de um eixo fixo com raio de 50 mm. Se o coeficiente de atrito cinético entre o eixo e a luva é , determine a força no segmento horizontal da correia de modo que a luva gire em sentido horário com velocidade angular constante. Suponha que a correia não deslize na luva, mas que esta deslize no eixo. Desconsidere os pesos e as espessuras. O raio, medido a partir do centro da luva até a espessura média da correia, é .
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Temos aqui um caso de mancal radial de deslizamento (a luva). Para esta questão, o nosso objetivo é calcular a força na correia para que a luva gire em sentido anti-horário com velocidade angular constante.
Uma dica é que esta questão é bem semelhante ao Exemplo 8.10. Podemos voltar sempre lá para rever os conceitos!
Mas, vamos ao que interessa. Se a luva gira no sentido anti-horário, temos o seguinte diagrama de corpo livre:
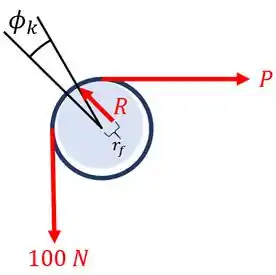
Com posse deste diagrama, vamos as contas!
Passo 2
Para que a gente descubra qual o valor de tal que a luva gire com velocidade angular constante, vamos ter que aplicar as equações de equilíbrio.
Então, vamos começar devagar. Primeiro vamos correlacionar a reação com as forças na correia. Separando nas componentes horizontal e vertical, temos:
E assim chegamos a e . Consequentemente, a reação será:
Passo 3
Para que a gente possa aplicar o somatório de momentos em torno de e enfim descubra qual o valor de , teremos que descobrir quem é antes.
Esta distância é tal que:
E assim, chegamos ao final da questão! Fazendo o somatório de momentos em torno de , temos:
Resolvendo a equação acima obtemos .
E assim finalizarmos a questão!