Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 8.Problemas - Ex. 115
A embreagem de disco é composta de uma placa plana que desliza sobre o eixo giratório , o qual é fixado na engrenagem motriz . Se a engrenagem , que está entrosada com , está sujeita a um torque , determine a menor força que deverá ser aplicada através do braço de controle para impedir a rotação. O coeficiente de atrito estático entre as placas e é . Suponha que a pressão de mancal entre e seja uniforme.
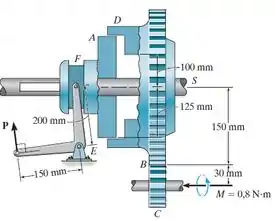
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
O objetivo desta questão é determinar a força no braço que faça com que o sistema pare de rotacionar.
Apesar da série de componentes, esta questão não é complicada. É só irmos trabalhando devagar que dará tudo certo!
Sendo assim, vamos começar determinando o torque que atua no eixo . Então, sabendo que o pinhão (engrenagem menor) está submetida a um torque , o torque na coroa (engrenagem maior), e consequentemente no eixo , será:
Passo 2
Agora temos que calcular qual a força axial necessária para parar um torque . E, para nossa alegria, esta fórmula já foi desenvolvida na seção 8.6! Então, temos apenas que aplicar a fórmula aqui.
Sendo assim, temos:
Só que nós queremos a força aplicada no braço de controle. Então, como o braço está estático, temos:
E assim finalizamos a questão!