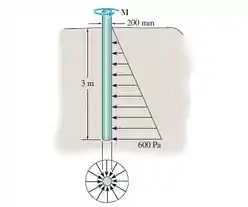
Um poste com diâmetro de 200 mm é afundado 3m na areia, para a qual . Se a pressão normal atuando completamente ao redor do poste varia linearmente com a profundidade, conforme mostrado, determine o torque de atrito que deve ser superado para girar o poste.

E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!

Temos que calcular o torque de atrito que deve ser superado para girar o poste.

Para que o poste fique na iminência de sair da inércia, é necessário que o torque seja igual ao momento gerado pela força de atrito. Como o poste possui um raio de , então, este torque será:

E agora, quem é esta força normal??? Ela é exatamente a resultante da pressão aplicado na lateral do poste. Calculando esta força, temos:

Então, o momento será:

E assim finalizarmos a questão!