Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 9.Problemas - Ex. 153
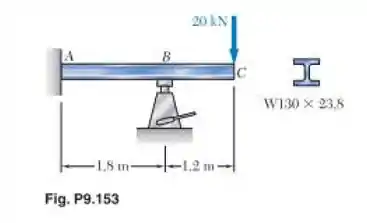
Um macaco hidráulico pode ser utilizado para elevar o ponto B da viga em balanço ABC. A viga era originalmente reta, horizontal e sem força aplicada. Foi aplicada então uma força de 20 kN no ponto C, fazendo esse ponto se mover para baixo. Determine (a) quanto o ponto B deve ser levantado para que o ponto C retorne à sua posição original e (b) o valor final da reação em B. Use E = 200 GPa.
Passo 1
Opaa! Fala pessoal, beleza? Bora pra mais um?! Para resolver esse exercício, vamos utilizar o método do momento de área. Para isso vamos precisar desenhar o diagrama M/EI para a viga. Depois disso, sabemos que a área entre dois pontos sob a curva M/EI representa a inclinação entre esses dois pontos. E para obter a deflexão, vamos utilizar o teorema do segundo momento de área, que nos fornece o desvio tangencial entre dois pontos. Sabendo disso, temos tudo o que precisamos para resolver o exercício, então bora lá!
Passo 2
Tá legal, vamos começar desenhando o DCL para uma seção da viga de comprimento , orientado da direita para a esquerda, para obter a expressão para o momento nessa parte, então teremos:
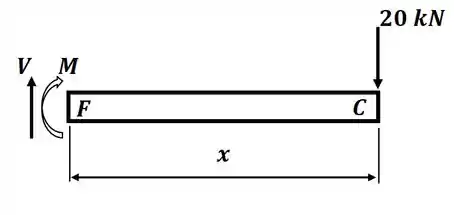
Então, nesse caso, aplicando o somatório de momento em relação ao ponto F, teremos:
Passo 3
Agora, estendendo a seção até algum ponto entre B e A, teremos o seguinte DCL:
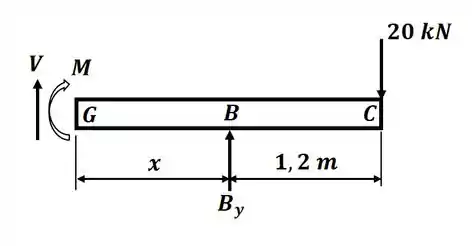
Então, nesse caso, aplicando o somatório de momento em relação ao ponto G, teremos:
Com as equações para o momento que encontramos, podemos dividir o momento em duas partes, o momento causado pela força localizada de 20 kN, que chamaremos de momento 1 e o causado pela reação de apoio em B, que chamaremos de momento 2, então teremos:
Passo 4
Agora vamos calcular os momentos nos pontos B e A para cada um deles, para que depois possamos desenhar o diagrama M/EI, então teremos:
Então nosso diagrama M/EI será:
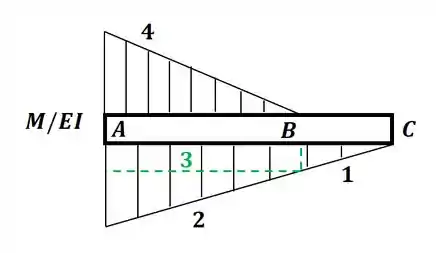
Agora vamos aproveitar e calcular o valor do termo EI, pois precisaremos dele para calcular a área do gráfico que encontramos. Então vamos começar indo lá no apêndice C para pegar o valor do momento de inércia para esse perfil de viga, onde teremos:
Então o nosso termo EI será:
Passo 5
Então, agora vamos calcular as áreas que encontramos e os seus centroides, então vamos lá:
Passo 6
Agora, para encontrar a reação em B, vamos utilizar a condição de deflexão de C com relação a A como sendo zero, já que queremos que ele retorne a sua posição original e sabemos que A não sofrerá deflexão. Então teremos:
Substituindo os valores encontrados, teremos:
Beleza, encontramos primeiro a resposta para a letra (b), bora pra letra (a) agora.
Passo 7
Agora, para descobrir o quanto o ponto B deve ser levantado, vamos utilizar o teorema do segundo momento de área entre os pontos B e A, onde teremos:
Substituindo os valores conhecidos, e sabendo que não temos deflexão no ponto A devido ao engaste, teremos:
Tooop! Terminamos mais um!!