Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 12.Problemas - Ex. 41

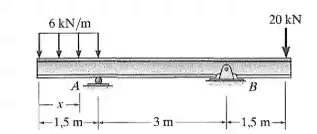
A viga está sujeita à carga mostrada na figura. Determine a equação da linha elástica. EI é constante.

Passo 1

Primeiro, devemos determinar as reações:

∑ M a = 0 →   9 × 0,75 - 20 × 4,5 + 3 V b = 0

V b = 27,75 k N

∑ F y = 0 → V a + V b - 9 - 20 = 0

V a = 1,25 k N

A equação do momento será:

M x = - 3 x 2 + 1,25 < x - 1,5 > + 3 < x - 1,5 > 2 + 27,75 < x - 4,5 >

Sabemos que:

E I d 2 v d x 2 = M x = - 3 x 2 + 1,25 < x - 1,5 > + 3 < x - 1,5 > 2 + 27,75 < x - 4,5 >

Integrando 2 vezes dos 2 lados, teremos:

E I v = - 0,25 x 4 + 0,20833 < x - 1,5 > 3 + 0,25 < x - 1,5 > 4 + 4,625 < x - 4,5 > 3 + C 1 x + C 2

Passo 2

As condições de contorno são:

x = 1,5 → v = 0

x = 4,5 → v = 0

Logo, teremos:

C 1 = 25,125 ; C 2 = - 36,42

Portanto, a equação da linha elástica será dada por:

v = 1 E I ( 0,25 x 4 + 0,20833 < x - 1,5 > 3 + 0,25 < x - 1,5 > 4 + 4,625 < x - 4,5 > 3 + 25,1 x - 36,4 )

Resposta

v = 1 E I ( 0,25 x 4 + 0,20833 < x - 1,5 > 3 + 0,25 < x - 1,5 > 4 + 4,625 < x - 4,5 > 3 + 25,1 x - 36,4 )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine as reações nos apoios e trace os diagramas de força cortante e momento fletor. EI é constante. O apoio B é um mancal de encosto.
Determine as reações ao momento nos apoios A e B; a seguir, trace os diagramas de força cortante e momento fletor. EI é constante.
Determine as reações ao momento nos apoios A e B; a seguir, trace os diagramas de força cortante e momento fletor. EI é constante.
A viga de madeira está sujeita à carga mostrada na figura. Considere que o apoio em A é um pino e em B, um rolete. Determine a inclinação em A e o deslocamento em C. Use o teorema dos momentos de área
A viga de madeira está sujeita à carga mostrada na figura. Considere que o apoio em A é um pino e em B, um rolete. Determine a inclinação em A e o deslocamento em C. Use o teorema dos momentos de área